题目内容
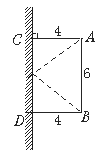
【题目】如图，A．B两点都与平面镜相距4米，且A．B两点相距6米，一束光线由A射向平面镜反射之后恰巧经过B点.求B点到入射点的距离.
【答案】5米
【解析】
试题作出B点关于CD的对称点B′，连结AB′，交CD于点O，则O点就是光的入射点，先根据“SSS”证得△B′DO≌△ACO，即可求得OC、OD的长，
连结OB，在Rt△ODB中，根据勾股定理即可求得结果.
作出B点关于CD的对称点B′，连结AB′，交CD于点O，则O点就是光的入射点.
因为B′D=DB.
所以B′D=AC.
∠B′DO=∠OCA=90°，
∠B′=∠CAO
所以△B′DO≌△ACO(SSS)
则OC=OD=
AB=×6=3米.
连结OB，在Rt△ODB中，OD2+BD2=OB2
所以OB2=32+42=52，即OB=5(米).
所以点B到入射点的距离为5米.
练习册系列答案
黄冈冠军课课练系列答案
相关题目
