题目内容
(1)人教版八年级数学下册92页第14题是这样叙述的:如图1,?ABCD中,过对角线BD上一点P作EF∥BC,HG∥AB,图中哪两个平行四边形的面积相等?为什么?
根据习题背景,写出面积相等的一对平行四边形的名称为______和______;
(2)如图2,点P为?ABCD内一点,过点P分别作AD、AB的平行线分别交?ABCD的四边于点E、F、G、H.已知S?BHPE=3,S?PFDG=5,则S△PAC=______;
(3)如图3,若①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH(不重复、无缝隙).已知①②③④四个平行四边形面积的和为14,四边形ABCD的面积为11,则菱形EFGH的周长为______.

解:(1)∵?ABCD中,EF∥BC,HG∥AB,
∴S△ABD=S△BCD,S△PBE=S△PBG,S△PDH=S△PDF,
∴S?AEPH=S?PGCF,S?ABGH=S?EBCF,S?AEFD=S?HGCD,
故答案为:?AEPH 和?PGCF 或?ABGH 和?EBCF 或?AEFD 和?HGCD;
(2)根据(1)可得:S△ABC=S△ADC,S△PAE=S△PAG,S△PCH=S△PCF,
∵S?BHPE=3,S?PFDG=5,
∴S△PAC=S△PAG+S△PCF+S?PFDG-S△ACD=S△PAG+S△PCF+S?PFDG- S?ABCD=S△PAG+S△PCF+S?PFDG-
S?ABCD=S△PAG+S△PCF+S?PFDG- (2S△PAG+2S△PCF+S?BHPE+S?PFDG)=S?PFDG-
(2S△PAG+2S△PCF+S?BHPE+S?PFDG)=S?PFDG- (S?BHPE+S?PFDG)=1;
(S?BHPE+S?PFDG)=1;
故答案为:1;
(3)∵①②③④四个平行四边形面积的和为14,
∴S1+S2+S3+S4=14,
∵四边形ABCD的面积为11,
∴S5=11-14× =4,
=4,
∴S菱形EFGH=S1+S2+S3+S4+S5=18,
∵菱形EFGH的一个内角为30°,
∴设边长为x,
则x•xsin30°=18,
解得:x=6,
∴菱形EFGH的周长为24.
故答案为:24.
分析:(1)由?ABCD中,EF∥BC,HG∥AB,根据平行四边形的性质,可得S△ABD=S△BCD,S△PBE=S△PBG,S△PDH=S△PDF,继而可得S?AEPH=S?PGCF,S?ABGH=S?EBCF,S?AEFD=S?HGCD;
(2)由(1)可得:S△ABC=S△ADC,S△PAE=S△PAG,S△PCH=S△PCF,继而可得S△PAC=S?PFDG- (S?BHPE+S?PFDG);
(S?BHPE+S?PFDG);
(3)由①②③④四个平行四边形面积的和为14,四边形ABCD的面积为11,即可求得菱形EFGH的面积,继而求得答案.
点评:此题考查了菱形的性质以及平行四边形的性质.此题难度较大,注意掌握数形结合思想与方程思想的应用.
∴S△ABD=S△BCD,S△PBE=S△PBG,S△PDH=S△PDF,
∴S?AEPH=S?PGCF,S?ABGH=S?EBCF,S?AEFD=S?HGCD,
故答案为:?AEPH 和?PGCF 或?ABGH 和?EBCF 或?AEFD 和?HGCD;
(2)根据(1)可得:S△ABC=S△ADC,S△PAE=S△PAG,S△PCH=S△PCF,
∵S?BHPE=3,S?PFDG=5,
∴S△PAC=S△PAG+S△PCF+S?PFDG-S△ACD=S△PAG+S△PCF+S?PFDG-
 S?ABCD=S△PAG+S△PCF+S?PFDG-
S?ABCD=S△PAG+S△PCF+S?PFDG- (2S△PAG+2S△PCF+S?BHPE+S?PFDG)=S?PFDG-
(2S△PAG+2S△PCF+S?BHPE+S?PFDG)=S?PFDG- (S?BHPE+S?PFDG)=1;
(S?BHPE+S?PFDG)=1;故答案为:1;
(3)∵①②③④四个平行四边形面积的和为14,
∴S1+S2+S3+S4=14,
∵四边形ABCD的面积为11,
∴S5=11-14×
 =4,
=4,∴S菱形EFGH=S1+S2+S3+S4+S5=18,
∵菱形EFGH的一个内角为30°,
∴设边长为x,
则x•xsin30°=18,
解得:x=6,
∴菱形EFGH的周长为24.
故答案为:24.
分析:(1)由?ABCD中,EF∥BC,HG∥AB,根据平行四边形的性质,可得S△ABD=S△BCD,S△PBE=S△PBG,S△PDH=S△PDF,继而可得S?AEPH=S?PGCF,S?ABGH=S?EBCF,S?AEFD=S?HGCD;
(2)由(1)可得:S△ABC=S△ADC,S△PAE=S△PAG,S△PCH=S△PCF,继而可得S△PAC=S?PFDG-
 (S?BHPE+S?PFDG);
(S?BHPE+S?PFDG);(3)由①②③④四个平行四边形面积的和为14,四边形ABCD的面积为11,即可求得菱形EFGH的面积,继而求得答案.
点评:此题考查了菱形的性质以及平行四边形的性质.此题难度较大,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目
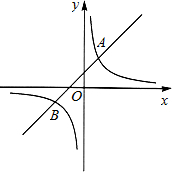 如图,已知反比例函数
如图,已知反比例函数 与一次函数y=x+b的图象在第一象限相交于点A(1,-k+4).解答下列问题:
与一次函数y=x+b的图象在第一象限相交于点A(1,-k+4).解答下列问题: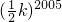 =________.
=________.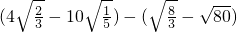 ;
;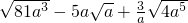 ;
;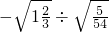 ;
;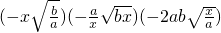 ;
;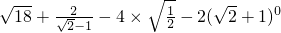 ;
;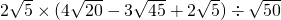 .
. 如图,半径分别为r与R的两圆相交(R≥r),那么两圆不重叠部分的面积的差是________.
如图,半径分别为r与R的两圆相交(R≥r),那么两圆不重叠部分的面积的差是________. 的频数是25,根据已知条件回答下列问题:
的频数是25,根据已知条件回答下列问题: