��Ŀ����
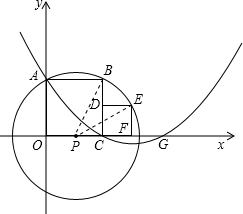
��2012•������һģ����ͼ���ֱ��������˴����ڵ�������OABC��CDEF�ı�OC��OA����ֱ��Ϊx�ᡢy�Ὠ��ƽ��ֱ������ϵ��C��F������x���������ϣ�������P��A��B��E���� ��Բ��P��x���ϣ���������y=
��Բ��P��x���ϣ���������y=
x2+bx+c����A��C���㣬��x�����һ����ΪG��������CDEF�����Ϊ4��
��1�����B�����ꣻ
��2���������ߵĽ���ʽ��
��3����ֱ��AC�������߶Գ��ύ�ڵ�N����Q�Ǵ˶Գ����ϲ����N�غϵ�һ���㣮
�����ACQ�ܳ�����Сֵ��
�����Q��������Ϊt����ACQ�����ΪS��ֱ��д��S��t֮��ĺ�����ϵʽ����ָ����Ӧ��t��ȡֵ��Χ��
 ��Բ��P��x���ϣ���������y=
��Բ��P��x���ϣ���������y=| 1 | 8 |
��1�����B�����ꣻ
��2���������ߵĽ���ʽ��
��3����ֱ��AC�������߶Գ��ύ�ڵ�N����Q�Ǵ˶Գ����ϲ����N�غϵ�һ���㣮
�����ACQ�ܳ�����Сֵ��
�����Q��������Ϊt����ACQ�����ΪS��ֱ��д��S��t֮��ĺ�����ϵʽ����ָ����Ӧ��t��ȡֵ��Χ��
��������1����ͼ�ף�����PE��PB����PC=n����������CDEF�����Ϊ4���ɵ�CD=CF=2������Բ�������εĶԳ���֪��OP=PC=n����PB=PE�����ݹ��ɶ����������n��ֵ���̶����B�����ꣻ
��2���ɣ�1��֪A��0��4����C��4��0����������������ߵĽ���ʽ��
��3������ͼ�ң��ӳ�AB����������A�䣬��CA�佻�Գ���x=6��Q����AQ������AQ=A��Q����ACQ�ܳ�����СֵΪAC+A��C�ij������ù��ɶ���������á�ACQ�ܳ�����Сֵ��
�ڷֱ�Q����F���Ϸ�ʱ����Q�����߶�FN��ʱ����Q����N���·�ʱȥ����������ô𰸣�
��2���ɣ�1��֪A��0��4����C��4��0����������������ߵĽ���ʽ��
��3������ͼ�ң��ӳ�AB����������A�䣬��CA�佻�Գ���x=6��Q����AQ������AQ=A��Q����ACQ�ܳ�����СֵΪAC+A��C�ij������ù��ɶ���������á�ACQ�ܳ�����Сֵ��
�ڷֱ�Q����F���Ϸ�ʱ����Q�����߶�FN��ʱ����Q����N���·�ʱȥ����������ô𰸣�
����⣺ ��1����ͼ������PE��PB����PC=n��
��1����ͼ������PE��PB����PC=n��
��������CDEF�����Ϊ4���ɵ�CD=CF=2��
����Բ�������εĶԳ���֪��OP=PC=n��
��PB=PE�����ݹ��ɶ�������
PB2=BC2+PC2=4n2+n2=5n2��
PE2=PF2+EF2=��n+2��2+4����5n2=��n+2��2+4
���n1=2��n2=-1����ȥ����
��BC=OC=4��
�ʵ�B������Ϊ��4��4����
��2���ɣ�1��A��0��4����C��4��0����
��������y=
x2+bx+c����A��C���㣬
��
���
����
�������ߵĽ���ʽΪy=
x2-
x+4��
��3������ͼ���ӳ�AB���������ڵ�A�䣬����CA�佻�Գ���x=6�ڵ�Q������AQ������AQ=A��Q����ACQ�ܳ�����СֵΪAC+A��C�ij���
���ù��ɶ�������Rt��AOC�У�AC=
=4
��
��Rt��A��BC��A��C=
=4
��
����ACQ�ܳ�����СֵΪ4
+4
��
��ֱ��AC�Ľ���ʽΪx+y-4=0����x=6ʱ��y=-2�����ڵ�Q��N���غϣ�
��t��-2��
��t��-2ʱ��
Q����F���Ϸ�ʱ��S=S����ACFK-S��AKQ-S��CFQ=
����6+2����2-
����4-t����6-
��t��2=2t-4��
ͬ������t��-2ʱ�ɵã���Q�����߶�FN��ʱ��S=-2t-4��
 ��1����ͼ������PE��PB����PC=n��
��1����ͼ������PE��PB����PC=n����������CDEF�����Ϊ4���ɵ�CD=CF=2��
����Բ�������εĶԳ���֪��OP=PC=n��
��PB=PE�����ݹ��ɶ�������
PB2=BC2+PC2=4n2+n2=5n2��
PE2=PF2+EF2=��n+2��2+4����5n2=��n+2��2+4
���n1=2��n2=-1����ȥ����
��BC=OC=4��
�ʵ�B������Ϊ��4��4����
��2���ɣ�1��A��0��4����C��4��0����
��������y=
| 1 |
| 8 |
��
|
���
|
�������ߵĽ���ʽΪy=
| 1 |
| 8 |
| 3 |
| 2 |
��3������ͼ���ӳ�AB���������ڵ�A�䣬����CA�佻�Գ���x=6�ڵ�Q������AQ������AQ=A��Q����ACQ�ܳ�����СֵΪAC+A��C�ij���
���ù��ɶ�������Rt��AOC�У�AC=
| AO2+OC2 |
| 2 |
��Rt��A��BC��A��C=
| A��B2+BC2 |
| 5 |
����ACQ�ܳ�����СֵΪ4
| 2 |
| 5 |
��ֱ��AC�Ľ���ʽΪx+y-4=0����x=6ʱ��y=-2�����ڵ�Q��N���غϣ�
��t��-2��
��t��-2ʱ��
Q����F���Ϸ�ʱ��S=S����ACFK-S��AKQ-S��CFQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
ͬ������t��-2ʱ�ɵã���Q�����߶�FN��ʱ��S=-2t-4��
���������⿼���˴���ϵ��������κ����Ľ���ʽ��Բ�����ʣ����������ε��ж��������Լ����ɶ�����֪ʶ�������ۺ��Ժ�ǿ����Ŀ�ѶȽϴ���Ĺؼ��Ƿ���˼�롢�������������ν��˼���Ӧ�ã�

��ϰ��ϵ�д�
 ����ѵ�����⿼ϵ�д�
����ѵ�����⿼ϵ�д�
�����Ŀ