题目内容
如图1,Rt△ABC中,∠A=90°,tanB= ,点P在线段AB上运动,点Q、R分别在线段BC、AC上,且使得四边形APQR是矩形,设AP的长为x,矩形APQR的面积为y,已知y是x的函数,其图象是过点(12,36)的抛物线的一部分(如图2所示)。
,点P在线段AB上运动,点Q、R分别在线段BC、AC上,且使得四边形APQR是矩形,设AP的长为x,矩形APQR的面积为y,已知y是x的函数,其图象是过点(12,36)的抛物线的一部分(如图2所示)。
 ,点P在线段AB上运动,点Q、R分别在线段BC、AC上,且使得四边形APQR是矩形,设AP的长为x,矩形APQR的面积为y,已知y是x的函数,其图象是过点(12,36)的抛物线的一部分(如图2所示)。
,点P在线段AB上运动,点Q、R分别在线段BC、AC上,且使得四边形APQR是矩形,设AP的长为x,矩形APQR的面积为y,已知y是x的函数,其图象是过点(12,36)的抛物线的一部分(如图2所示)。
(1)求AB的长;
(2)当AP为何值时,矩形APQR的面积最大,并求出最大值。
为了解决这个问题,孔明和研究性学习小组的同学作了如下讨论:
张明:图2中的抛物线过点(12,36)在图1中表示什么呢?
李明:因为抛物线上的点(x,y)是表示图1中AP的长与矩形APQR面积的对应关系,那么,(12,36)表示当AP=12时,AP的长与矩形APQR面积的对应关系。
赵明:对,我知道纵坐标36是什么意思了!
孔明:哦,这样就可以算出AB,这个问题就可以解决了。
请根据上述对话,帮他们解答这个问题。
(2)当AP为何值时,矩形APQR的面积最大,并求出最大值。
为了解决这个问题,孔明和研究性学习小组的同学作了如下讨论:
张明:图2中的抛物线过点(12,36)在图1中表示什么呢?
李明:因为抛物线上的点(x,y)是表示图1中AP的长与矩形APQR面积的对应关系,那么,(12,36)表示当AP=12时,AP的长与矩形APQR面积的对应关系。
赵明:对,我知道纵坐标36是什么意思了!
孔明:哦,这样就可以算出AB,这个问题就可以解决了。
请根据上述对话,帮他们解答这个问题。
解:(1)当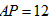 时,
时,

∴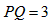 ,
,
又在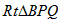 中,
中,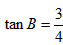 ,
,
∴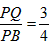
∴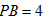
∴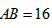 ;
;
(2)若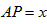 ,则
,则 ,
,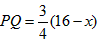 ,
,
∴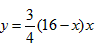 ,
,
整理得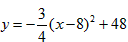 ,
,
∴ 当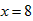 时,
时, 。
。
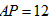 时,
时, 
∴
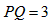 ,
,又在
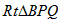 中,
中,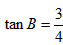 ,
,∴
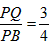
∴
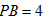
∴
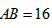 ;
;(2)若
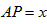 ,则
,则 ,
,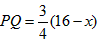 ,
,∴
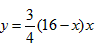 ,
,整理得
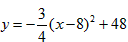 ,
,∴ 当
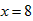 时,
时, 。
。 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•和平区二模)如图,在Rt△ABC中,∠BAC=90°,AB=6,AM为∠BAC的平分线,CM=2BM.下列结论:
(2012•和平区二模)如图,在Rt△ABC中,∠BAC=90°,AB=6,AM为∠BAC的平分线,CM=2BM.下列结论: (2013•遵义)如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,E为BC边上的一点,以A为圆心,AE为半径的圆弧交AB于点D,交AC的延长于点F,若图中两个阴影部分的面积相等,则AF的长为
(2013•遵义)如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,E为BC边上的一点,以A为圆心,AE为半径的圆弧交AB于点D,交AC的延长于点F,若图中两个阴影部分的面积相等,则AF的长为 如图,在Rt△ABC中,∠C=90°,∠A=30°,AB+BC=9cm,则AB的长为( )
如图,在Rt△ABC中,∠C=90°,∠A=30°,AB+BC=9cm,则AB的长为( ) 的外接圆.
的外接圆. (2013•嘉定区二模)如图,在Rt△ABC中,∠ACB=90°,点D在AC边上,且BC2=CD•CA.
(2013•嘉定区二模)如图,在Rt△ABC中,∠ACB=90°,点D在AC边上,且BC2=CD•CA.