题目内容
 (2012•和平区二模)如图,在Rt△ABC中,∠BAC=90°,AB=6,AM为∠BAC的平分线,CM=2BM.下列结论:
(2012•和平区二模)如图,在Rt△ABC中,∠BAC=90°,AB=6,AM为∠BAC的平分线,CM=2BM.下列结论:①tan∠MAC=
| ||
| 2 |
| AC |
| CM |
| BC |
| CA |
| CM |
| AB |
| 2 |
其中不正确结论的序号是
①③④⑤
①③④⑤
.分析:①利用特殊角的三角函数值来解答;
②通过作辅助线MD、MN构造正方形ADMN,相似三角形△CNM∽△CAB,然后利用正方形的性质、相似三角形的对应边成比例求得DM,即点M到AB的距离;
③利用角平分线定理和勾股定理求得AC=12,BC=6
,然后由已知条件来证明
=
是否成立;
④由③中的直角△ABC的三边的长度、三角形内角和定理,利用反证法来证明∠B=2∠C是否成立;
⑤由③中的直角△ABC的三边的长度来求
的值.
②通过作辅助线MD、MN构造正方形ADMN,相似三角形△CNM∽△CAB,然后利用正方形的性质、相似三角形的对应边成比例求得DM,即点M到AB的距离;
③利用角平分线定理和勾股定理求得AC=12,BC=6
| 5 |
| AC |
| CM |
| BC |
| CA |
④由③中的直角△ABC的三边的长度、三角形内角和定理,利用反证法来证明∠B=2∠C是否成立;
⑤由③中的直角△ABC的三边的长度来求
| CM |
| AB |
解答: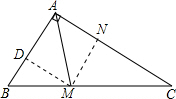 解:如图所示:过点M作MN∥AB于点N、MD∥AC于点D.则四边形ADMN是矩形.
解:如图所示:过点M作MN∥AB于点N、MD∥AC于点D.则四边形ADMN是矩形.
①tan∠MAC=tan45°=1;
故本选项错误;
②∵在Rt△ABC中,∠BAC=90°,AM为∠BAC的平分线,
∴∠NAM=45°,
∴∠NMA=45°,
∴∠NAM=∠NMA,
∴AN=MN.
∴矩形ADMN是正方形.
∵△CNM∽△CAB,
∴
=
.
又∵AB=6,CM=2BM,
∴MN=4,
∴DM=MN=4,即点M到AB的距离是4;
故本选项正确;
③∵AM为∠BAC的平分线,AB=6,CM=2BM,
∴
=
,即
=2,
解得,AC=12.
则在Rt△ABC中,由勾股定理知,BC=
=
=6
,
∴
=
=
×
=
,
=
=
,
∵
≠
,
∴
≠
;
故本选项错误;
④若∠B=2∠C时,∠C=30°,则BC=2AB=12,这与BC=6
相矛盾;故本选项错误;
⑤∵BC=6
,CM=2BM,
∴CM=
BC=4
,
∴
=
=
;
故本选项错误;
综上所述,错误的说法是:①③④⑤;
故答案是:①③④⑤.
 解:如图所示:过点M作MN∥AB于点N、MD∥AC于点D.则四边形ADMN是矩形.
解:如图所示:过点M作MN∥AB于点N、MD∥AC于点D.则四边形ADMN是矩形.①tan∠MAC=tan45°=1;
故本选项错误;
②∵在Rt△ABC中,∠BAC=90°,AM为∠BAC的平分线,
∴∠NAM=45°,
∴∠NMA=45°,
∴∠NAM=∠NMA,
∴AN=MN.
∴矩形ADMN是正方形.
∵△CNM∽△CAB,
∴
| MN |
| AB |
| MC |
| BC |
又∵AB=6,CM=2BM,
∴MN=4,
∴DM=MN=4,即点M到AB的距离是4;
故本选项正确;
③∵AM为∠BAC的平分线,AB=6,CM=2BM,
∴
| AC |
| AB |
| CM |
| BM |
| AC |
| 6 |
解得,AC=12.
则在Rt△ABC中,由勾股定理知,BC=
| AB2+AC2 |
| 62+122 |
| 5 |
∴
| AC |
| CM |
| AC | ||
|
| 3 |
| 2 |
| 12 | ||
6
|
3
| ||
| 5 |
| BC |
| CA |
6
| ||
| 12 |
| ||
| 2 |
∵
3
| ||
| 5 |
| ||
| 2 |
∴
| AC |
| CM |
| BC |
| CA |
故本选项错误;
④若∠B=2∠C时,∠C=30°,则BC=2AB=12,这与BC=6
| 5 |
⑤∵BC=6
| 5 |
∴CM=
| 2 |
| 3 |
| 5 |
∴
| CM |
| AB |
4
| ||
| 6 |
2
| ||
| 3 |
故本选项错误;
综上所述,错误的说法是:①③④⑤;
故答案是:①③④⑤.
点评:本题考查了相似三角形的判定与性质,角平分线的性质以及特殊角的三角函数值.已知一条直线平行于三角形的一边,与另两边(或延长线)相交形成的三角形与原三角形相似,且相似三角形的对应边成比例.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案
相关题目
 (2012•和平区二模)如图,点P是菱形ABCD的对角线AC上一动点(不与点A、C重合).过点P且垂直于AC的直线交菱形ABCD的边于M、N两点.若AC=2,BD=1,设AP=x,S△AMN=y,则y关于x的函数图象的大致形状是( )
(2012•和平区二模)如图,点P是菱形ABCD的对角线AC上一动点(不与点A、C重合).过点P且垂直于AC的直线交菱形ABCD的边于M、N两点.若AC=2,BD=1,设AP=x,S△AMN=y,则y关于x的函数图象的大致形状是( ) (2012•和平区二模)如图,在直角坐标系中,O为坐标原点.已知反比例函数
(2012•和平区二模)如图,在直角坐标系中,O为坐标原点.已知反比例函数 (2012•和平区二模)如图,在Rt△ADC中,∠ADC=90°,以CD为直径的半圆O交AC于点E,点G是AD的中点.
(2012•和平区二模)如图,在Rt△ADC中,∠ADC=90°,以CD为直径的半圆O交AC于点E,点G是AD的中点.