题目内容
【题目】疫情期间,某销售商在网上销售A、B两种型号的电脑“手写板”,其进价、售价和每日销量如下表所示:
进价(元/个) | 售价(元/个) | 销量(个/日) | |
A型 | 400 | 600 | 200 |
B型 | 800 | 1200 | 400 |
根据市场行情,该销售商对A型手写板降价销售,同时对B型手写板提高售价,此时发现A型手写板每降低5元就可多卖1个,B型手写板每提高5元就少卖1个.销售时保持每天销售总量不变,设其中A型手写板每天多销售x个,每天获得的总利润为y元.
(1)求y与x之间的函数关系式,并直接写出x的取值范围;
(2)要使每天的利润不低于212000元,求出x的取值范围;
(3)该销售商决定每销售一个B型手写板,就捐助a元![]() 给受“新冠疫情”影响的困难学生,若当30≤x≤40时,每天的最大利润为203400元,求a的值.
给受“新冠疫情”影响的困难学生,若当30≤x≤40时,每天的最大利润为203400元,求a的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据“总利润=A型手写板利润+B型手写板利润”即可确定函数解析式;根据600-400-5x≥0,1200-800+5x≥0即可确定自变量取值范围;
(2)把y=212000,代入函数解析式求出x值,根据函数增减性结合(1)自变量取值,即可求出x的取值;
(3)设捐款后每天的利润为w元,则w=-10x2+800x+200000-(400-x)a,即可得到w与x的关系式,确定对称轴为![]() ,结合
,结合![]() 确定对称轴取值范围
确定对称轴取值范围![]() ,结合抛物线的性质即可求出当x=40时,w最大,进而求出a.
,结合抛物线的性质即可求出当x=40时,w最大,进而求出a.
解:(1)由题意得,y=(600-400-5x)(200+x)+(1200-800+5x)(400-x)
=-10x2+800x+200000,(0≤x≤40且x为整数)
(写0<x≤40且x为整数,不扣分)
(2)x的取值范围为20≤x≤40.
理由如下:y=-10x2+800x+200000=-10(x-40)2+216000,
当y=212000时,-10(x-40)2+216000=212000,
(x-40)2=4000,x-40=±20,
解得:x=20或x=60.
要使y≥212000,
得20≤x≤60;
∵0≤x≤40,
∴20≤x≤40;
(3)设捐款后每天的利润为w元,则
w=-10x2+800x+200000-(400-x)a=-10x2+(800+a)x+200000-400a,
对称轴为![]() ,
,
∵0<a≤100,
∴![]() ,
,
∵抛物线开口向下,当30≤x≤40时,w随x的增大而增大,
当x=40时,w最大,
∴-16000+40(800+a)+200000-400a=203400,
解得a=35.

 阅读快车系列答案
阅读快车系列答案【题目】已知:点A、点B在直线![]() 的两侧.
的两侧.
(点A到直线![]() 的距离小于点B到直线
的距离小于点B到直线![]() 的距离).
的距离).
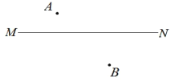
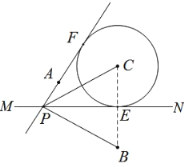
如图, (1)作点B关于直线 (2)以点C为圆心, (3)过点A作 (4)连接 |
|
根据以上作图过程及所作图形,下列四个结论中:
①![]() 是
是![]() 的切线; ②
的切线; ②![]() 平分
平分![]() ;
;
③![]() ; ④
; ④![]() .
.
所有正确结论的序号是___________________________.