题目内容
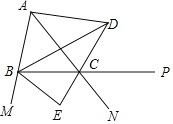
【题目】如图:AE⊥AB,AF⊥AC,AE=AB,AF=AC,
(1)图中EC、BF有怎样的数量和位置关系?试证明你的结论.
(2)连接AM,求证:MA平分∠EMF.

【答案】(1)结论:EC=BF,EC⊥BF.理由详见解析;(2)详见解析.
【解析】
(1)先由条件可以得出∠EAC=∠BAE,再证明△EAC≌△BAF就可以得出结论;
(2)作AP⊥CE于P,AQ⊥BF于Q.由△EAC≌△BAF,推出AP=AQ(全等三角形对应边上的高相等).由AP⊥CE于P,AQ⊥BF于Q,可得AM平分∠EMF.
(1)结论:EC=BF,EC⊥BF,
理由:∵AE⊥AB,AF⊥AC,
∴∠EAB=∠CAF=90°,
∴∠EAB+∠BAC=∠CAF+∠BAC,
∴∠EAC=∠BAE,
在△EAC和△BAF中,
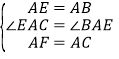 ,
,
∴△EAC≌△BAF(SAS),
∴EC=BF.∠AEC=∠ABF
∵∠AEG+∠AGE=90°,∠AGE=∠BGM,
∴∠ABF+∠BGM=90°,
∴∠EMB=90°,
∴EC⊥BF.
∴EC=BF,EC⊥BF;
(2)作AP⊥CE于P,AQ⊥BF于Q,
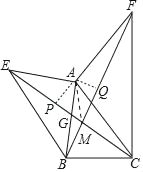
∵△EAC≌△BAF,
∴AP=AQ(全等三角形对应边上的高相等)
∵AP⊥CE于P,AQ⊥BF于Q,
∴AM平分∠EMF.

练习册系列答案
相关题目