题目内容
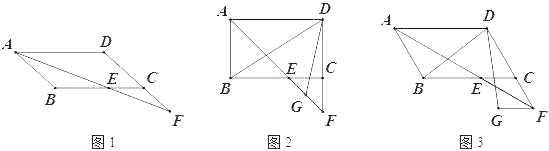
【题目】在△ABC中,∠BAC=90°,AB=AC,点D是边BC上一动点,连接AD,过点A作AE⊥AD,且AE=AD,连接CE.

(1)如图,求证:BD=CE;
(2)若AF平分∠DAE交直线BC于点F.
①如图,当点F在线段BC上,猜想线段BD,DF,FC之间的数量关系,并证明;
②若BD=6,CF=8,直接写出AD的长.
【答案】(1)证明见解析;(2)①BD2+FC2=DF2,证明见解析;②6![]() 或
或![]()
【解析】
(1)根据SAS,只要证明∠1=∠2即可求得△ABD≌△ACE,从而解决问题;
(2)①连接FE,想办法证明∠ECF=90°,EF=DF,利用勾股定理即可解决问题;
②过点A作AG⊥BC于G,在Rt△ADG中,想办法求出AG、DG即可解决问题.
解:(1)∵AE⊥AD,
∴∠DAE=∠DAC+∠2=90°,
又∵∠BAC=∠DAC+∠1=90°,
∴∠1=∠2,
在△ABD和△ACE中 
∴△ABD≌△ACE
∴BD=CE
(2)结论:BD2+FC2=DF2.理由如下:
连接FE,∵∠BAC=90°,AB=AC,
∴∠B=∠3=45°
由(1)知△ABD≌△ACE
∴∠4=∠B=45°,BD=CE
∴∠ECF=∠3+∠4=90°,
∴CE2+CF2=EF2,
∴BD2+FC2=EF2,
∵AF平分∠DAE,
∴∠DAF=∠EAF,
在△DAF和△EAF中 ,
,
∴△DAF≌△EAF
∴DF=EF
∴BD2+FC2=DF2.
(3)如图,过点A作AG⊥BC于G,
由(2)知DF2=BD2+FC2=62+82=100.
∴DF=10,
当点F在线段BC上时,BC=BD+DF+FC=6+10+8=24,
∵AB=AC,AG⊥BC,
∴BG=AG=![]() BC=12,
BC=12,
∴DG=BG-BD=12-6=6,
∴在Rt△ADG中,AD=![]()
当点F在线段BC的延长线上时,BC=BD+DF-FC=6+10-8=8,
∵AB=AC,AG⊥BC,
∴BG=AG=![]() BC=4,
BC=4,
∴DG= BD- BG=6-4=2,
∴在Rt△ADG中,AD=![]()
综上,AD的长为![]() 或
或![]()