题目内容
(1)一元二次方程x2-2x+1=0的两根是x1=______,x2=______;2x2-3x+1=0的两根是x1=______,x2=______;6x2+7x+2=0的两根是x1=______,x2=______.
(2)由(1)中一元二次方程的两根,请你猜想:若一元二次方程ax2+bx+c=0有两个实数根x1,x2与系数a,b,c之间的关系是:x1+x2=______,x1x2=______.
(3)设一元二次方程2x2-5x+1=0的两根分别为x1,x2,不解方程,利用(2)中的结论,求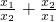 的值.
的值.
解:(1)方程x2-2x+1=0,分解因式得:(x-1)2=0,
开方得:x-1=0,
解得:x1=x2=1;
方程2x2-3x+1=0,分解因式得:(2x-1)(x-1)=0,
可得:2x-1=0或x-1=0,
解得:x1=1,x2= ;
;
方程6x2+7x+2=0,分解因式得:(3x+2)(2x+1)=0,
可得:3x+2=0或2x+1=0,
解得:x1=- ,x2=-
,x2=- ;
;
(2)方程x2-2x+1=0的x1+x2=2=-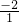 ,x1x2=1=
,x1x2=1= ;
;
方程2x2-3x+1=0的x1+x2= =-
=-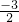 ,x1x2=
,x1x2= ;
;
方程6x2+7x+2=0的x1+x2=- ,x1x2=
,x1x2= =
=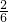 ,
,
则一元二次方程ax2+bx+c=0有两个实数根x1,x2,
有x1+x2=- ,x1x2=
,x1x2= ;
;
(3)∵x1+x2=-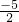 =
= ,x1x2=
,x1x2= ,
,
∴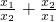 =
=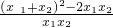 =
= .
.
故答案为:(1)1,1;1, ;
; ,
, ;(2)
;(2) ,
,
分析:(1)第一个方程左边利用完全平方公式分解因式,第二、三个方程利用十字相乘法分解因式,然后分别利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程,求出一次方程的解即可得到各自的解;
(2)求出每一个方程的两根之和与两根之积,归纳总结得到一元二次方程ax2+bx+c=0的两根之和与两根之积即可;
(3)找出方程中的a,b及c的值,利用第二问猜想的结论,求出x1+x2与x1x2的值,然后将所求式子通分并利用同分母分式的加法法则变形后,把x1+x2与x1x2的值代入即可求出值.
点评:此题考查了根与系数的关系,一元二次方程ax2+bx+c=0(a≠0),当b2-4ac<0时,方程无解;当b2-4ac≥0时,方程有解,当方程有解时,设方程两解分别为x1,x2,则有x1+x2=- ,x1x2=
,x1x2= .
.
开方得:x-1=0,
解得:x1=x2=1;
方程2x2-3x+1=0,分解因式得:(2x-1)(x-1)=0,
可得:2x-1=0或x-1=0,
解得:x1=1,x2=
 ;
;方程6x2+7x+2=0,分解因式得:(3x+2)(2x+1)=0,
可得:3x+2=0或2x+1=0,
解得:x1=-
 ,x2=-
,x2=- ;
;(2)方程x2-2x+1=0的x1+x2=2=-
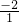 ,x1x2=1=
,x1x2=1= ;
;方程2x2-3x+1=0的x1+x2=
 =-
=-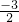 ,x1x2=
,x1x2= ;
;方程6x2+7x+2=0的x1+x2=-
 ,x1x2=
,x1x2= =
=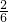 ,
,则一元二次方程ax2+bx+c=0有两个实数根x1,x2,
有x1+x2=-
 ,x1x2=
,x1x2= ;
;(3)∵x1+x2=-
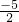 =
= ,x1x2=
,x1x2= ,
,∴
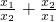 =
=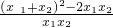 =
= .
.故答案为:(1)1,1;1,
 ;
; ,
, ;(2)
;(2) ,
,
分析:(1)第一个方程左边利用完全平方公式分解因式,第二、三个方程利用十字相乘法分解因式,然后分别利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程,求出一次方程的解即可得到各自的解;
(2)求出每一个方程的两根之和与两根之积,归纳总结得到一元二次方程ax2+bx+c=0的两根之和与两根之积即可;
(3)找出方程中的a,b及c的值,利用第二问猜想的结论,求出x1+x2与x1x2的值,然后将所求式子通分并利用同分母分式的加法法则变形后,把x1+x2与x1x2的值代入即可求出值.
点评:此题考查了根与系数的关系,一元二次方程ax2+bx+c=0(a≠0),当b2-4ac<0时,方程无解;当b2-4ac≥0时,方程有解,当方程有解时,设方程两解分别为x1,x2,则有x1+x2=-
 ,x1x2=
,x1x2= .
. 
练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
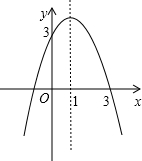 已知二次函数y=-x2+bx+c的图象如图所示,解决下列问题:
已知二次函数y=-x2+bx+c的图象如图所示,解决下列问题: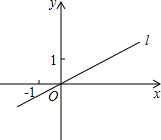 如图,在平面直角坐标系中,直线l的解析式为y=
如图,在平面直角坐标系中,直线l的解析式为y=