题目内容
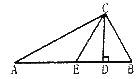
【题目】如图,CD是△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处.

(1)求∠A的度数;
(2)若![]() ,求△AEC的面积.
,求△AEC的面积.
【答案】 (1)∠A的度数为30°; (2) △AEC面积为![]() .
.
【解析】分析:(1)根据直角三角形斜边上的中线等于斜边的一半可得到AC=AE,从而得到∠A=∠ACE,再由折叠的性质及三角形的外角性质得到∠B=2∠A,从而不难求得∠A的度数.(2)由(1)得∠A=30°,据解直角三角形得△CEB是等边三角形,继而求解.
本题解析:(1)∵E是AB中点,∴CE为Rt△ACB斜边AB上的中线。AE=BE=CE=![]() AB,。
AB,。
∵CE=CB.∴△CEB为等边三角形。
∴ ∠CEB=60°。 ∵ CE=AE.∴∠A=∠ACE=30°。
故∠A的度数为30°。
(2)∵Rt△ACB中,∠A=30°,∴tanA![]() ,
,
∴ AC=![]() ,BC=1,∴△CEB是等边三角形,CD⊥BE,∴CD=
,BC=1,∴△CEB是等边三角形,CD⊥BE,∴CD=![]() ,
,
∵AB=2BC=2,∴![]() ,∴S△ACE=
,∴S△ACE=![]() ,
,
即△AEC面积为![]() 。
。

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目