题目内容
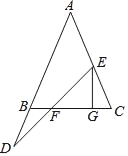
【题目】如图,∠ABC=∠C,点E在线段AC上,D在AB的延长线上,且有BD=CE,连接DE交BC于F,过E作FG⊥BC于G.试说明线段EF、FG、CG之间的数量关系.
【答案】见解析
【解析】试题分析:在BC上截取GH=GC,可得△EHC是等腰三角形,进而得出AB∥EH,再证△BDF≌△HEF,通过线段之间的转化即可得出结论.
试题解析:在BC上截取GH=GC,连接EH,
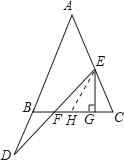
∵EG⊥BC,GH=GC,
∴EH=EC,
∴∠EHC=∠C,
又AB=AC,
∴∠ABC=∠C,
∴∠EHC=∠ABC,
∴EH∥AB,
∴∠DBF=∠EHF,∠D=∠DEH,
又EH=EC=BD,
∴△BDF≌△HEF,
∴BF=FH,
∴FG=FH+HG=BF+GC.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目