题目内容
【题目】如图,菱形ABCD中,
(1)若半径为1的⊙O经过点A、B、D,且∠A=60°,求此时菱形的边长;
(2)若点P为AB上一点,把菱形ABCD沿过点P的直线a折叠,使点D落在BC边上,利用无刻度的直尺和圆规作出直线a.(保留作图痕迹,不必说明作法和理由)

【答案】(1)菱形的边长为![]() ;
;
(2)作图见解析.
【解析】试题分析:(1)连接OB、OD和OC,根据菱形、内接圆的性质可得∠DOB=120°,OD=OB=1, CD=BC,∠C=60°,从而得到△COD≌△COB,根据全等三角形的性质,可求得∠COD=∠COB=![]() 、∠DCO=∠BCO=
、∠DCO=∠BCO=![]() ,根据三角形内角和可得△COD 是Rt△COD,由tan∠DCO=
,根据三角形内角和可得△COD 是Rt△COD,由tan∠DCO=![]() 可求得CD的长度,即为所求;(2)根据题意先作出D在BC上的对应点;作出直线a;
可求得CD的长度,即为所求;(2)根据题意先作出D在BC上的对应点;作出直线a;
试题解析:
(1)连接OB、OD和OC,如图所示:

∵半径为1的⊙O经过点A、B、D,且∠A=60°,
∴∠DOB=120°,OD=OB=1,
∵四边形ABCD是菱形,∠A=60°,
∴CD=BC,∠C=60°,
在△COD和△COB中

∴△COD≌△COB(SSS),
∴∠COD=∠COB,∠DCO=∠BCO,
∴∠COD=∠COB=![]() ,
,
∠DCO=∠BCO=![]()
∴∠ODC=(180-30-60)o=90o,
∴△COD 是Rt△COD,
∵tan∠DCO=![]()
∴CD=tan30o![]()
∴菱形ABCD的边长是![]() ;
;
(2)如图所示:
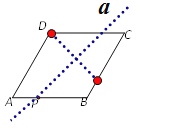
作出D在BC上的对应点,再作出直线a即可。

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目

