题目内容
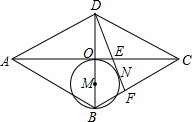
【题目】如图,在△ABC中,∠BAC=50°,把△ABC沿EF折叠,C对应点恰好与△ABC的外心O重合,则∠CFE的度数是( ) 
A.40°
B.45°
C.50°
D.55°
【答案】C
【解析】解:连接OB、OC,如图所示: 由圆周角定理得:∠BOC=2∠BAC=100°,
∵OB=OC,
∴∠OCF= ![]() (180°﹣100°)=40°,
(180°﹣100°)=40°,
由折叠的性质得:OC⊥EF,
∴∠CFE=90°﹣40°=50°;
故选:C.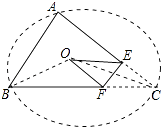
【考点精析】掌握三角形的外接圆与外心和翻折变换(折叠问题)是解答本题的根本,需要知道过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.

练习册系列答案
相关题目
【题目】探究多边形内角和问题.
连接多边形不相邻的两个顶点的线段叫做多边形的对角线.从多边形某一个顶点出发的×对角线可以把一个多边形分成几个三角形.这样就把多边形内角和问题转化为三角形内角和问题了.
(1)请你试一试,做一做,把下面表格补充完整:
名称 | 图形 | 内角和 |
三角形 |
| 180° |
四边形 |
| 2×180°=360° |
五边形 |
|
|
六边形 |
|
|
… | … | … |
根据表格探究发现的规律,完成下面的问题:
(2)七边形的内角和等于 度;
(3)如果一个多边形有n条边,请你用含有n的代数式表示这个多边形的内角和: .