题目内容
【题目】如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于点D,DE⊥AD且与AC的延长线交于点E.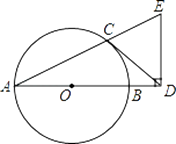
(1)求证:DC=DE;
(2)若tan∠CAB= ![]() ,AB=3,求BD的长.
,AB=3,求BD的长.
【答案】
(1)
证明:连接OC,
∵CD是⊙O的切线,
∴∠OCD=90°,
∴∠ACO+∠DCE=90°,
又∵ED⊥AD,∴∠EDA=90°,
∴∠EAD+∠E=90°,
∵OC=OA,∴∠ACO=∠EAD,
故∠DCE=∠E,
∴DC=DE,
(2)
解:设BD=x,则AD=AB+BD=3+x,OD=OB+BD=1.5+x,
在Rt△EAD中,
∵tan∠CAB= ![]() ,∴ED=
,∴ED= ![]() AD=
AD= ![]() (3+x),
(3+x),
由(1)知,DC= ![]() (3+x),在Rt△OCD中,
(3+x),在Rt△OCD中,
OC2+CD2=DO2,
则1.52+[ ![]() (3+x)]2=(1.5+x)2,
(3+x)]2=(1.5+x)2,
解得:x1=﹣3(舍去),x2=1,
故BD=1.
【解析】(1)根据“等角对等边”,从证∠DCE=∠E出发,连接OC,根据两个直角,去找相关角的数量关系;
(2)根据勾股定理构造方程去解.

练习册系列答案
相关题目