��Ŀ����
����֪���ٷ������Ի�Ϊ�����������磺
=2+
=2
���ڷ�ʽ�У�����ֻ����һ����ĸ�ķ�ʽ�������ӵĴ������ڻ���ڷ�ĸ�Ĵ���ʱ�����dz�֮Ϊ���ٷ�ʽ���������ӵĴ���С�ڷ�ĸ�Ĵ���ʱ�����dz�֮Ϊ�����ʽ�������磺
��
�����ķ�ʽ���Ǽٷ�ʽ��
��
�����ķ�ʽ�������ʽ�����Ƶģ��ٷ�ʽҲ���Ի�Ϊ����ʽ������ʽ�����ʽ�͵���ʽ����
���磺
=
=1-
��
=
=
=x+1+
��
��1������ʽ
��Ϊ����ʽ��
��2������ʽ
��ֵΪ��������x������ֵ��
| 8 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| x-1 |
| x+1 |
| x2 |
| x-1 |
| 3 |
| x+1 |
| 2x |
| x2+1 |
���磺
| x-1 |
| x+1 |
| (x+1)-2 |
| x+1 |
| 2 |
| x+1 |
| x2 |
| x-1 |
| x2-1+1 |
| x-1 |
| (x+1)(x-1)+1 |
| x-1 |
| 1 |
| x-1 |
��1������ʽ
| x-1 |
| x+2 |
��2������ʽ
| 2x-1 |
| x+1 |
��������1���������е��Ķ����Ͻ�ԭʽ��Ϊ����ʽ���ɣ�
��2���������е��Ķ����Ͻ�ԭʽ��Ϊ����ʽ�����ݽ��Ϊ������ȷ����x������ֵ���ɣ�
��2���������е��Ķ����Ͻ�ԭʽ��Ϊ����ʽ�����ݽ��Ϊ������ȷ����x������ֵ���ɣ�
����⣺��1��
=
=1-
��
��2��
=
=2-
��
��
Ϊ����ʱ��
ҲΪ������
��x+1��ȡ�õ�����ֵΪ��1����3��
��x�Ŀ�������ֵΪ0��-2��2��-4��
| x-1 |
| x+2 |
=
| (x+2)-3 |
| x+2 |
=1-
| 3 |
| x+2 |
��2��
| 2x-1 |
| x+1 |
| 2(x+1)-3 |
| x+1 |
| 3 |
| x+1 |
��
| 2x-1 |
| x+1 |
| 3 |
| x+1 |
��x+1��ȡ�õ�����ֵΪ��1����3��
��x�Ŀ�������ֵΪ0��-2��2��-4��
���������⿼���˷�ʽ�Ļ�����㣬�����������㷨���ǽⱾ��Ĺؼ���

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
 =
=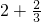 =
=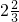 ���ڷ�ʽ�У�����ֻ����һ����ĸ�ķ�ʽ�������ӵĴ������ڻ���ڷ�ĸ�Ĵ���ʱ�����dz�֮Ϊ���ٷ�ʽ���������ӵĴ���С�ڷ�ĸ�Ĵ���ʱ�����dz�֮Ϊ�����ʽ�������磺
���ڷ�ʽ�У�����ֻ����һ����ĸ�ķ�ʽ�������ӵĴ������ڻ���ڷ�ĸ�Ĵ���ʱ�����dz�֮Ϊ���ٷ�ʽ���������ӵĴ���С�ڷ�ĸ�Ĵ���ʱ�����dz�֮Ϊ�����ʽ�������磺 ��
��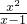 �����ķ�ʽ���Ǽٷ�ʽ��
�����ķ�ʽ���Ǽٷ�ʽ��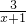 ��
��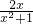 �����ķ�ʽ�������ʽ�����Ƶģ��ٷ�ʽҲ���Ի�Ϊ����ʽ��������ʽ�����ʽ�͵���ʽ����
�����ķ�ʽ�������ʽ�����Ƶģ��ٷ�ʽҲ���Ի�Ϊ����ʽ��������ʽ�����ʽ�͵���ʽ����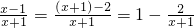 ��
�� 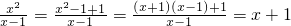 +
+ ��
��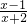 ��Ϊ����ʽ��
��Ϊ����ʽ��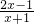 ��ֵΪ��������x������ֵ��
��ֵΪ��������x������ֵ��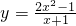 ͼ�������к��������Ϊ�����ĵ�����꣮
ͼ�������к��������Ϊ�����ĵ�����꣮