题目内容
我们知道,假分数可以化为带分数.例如: =
=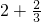 =
=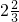 .在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.例如:
.在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.例如: ,
,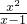 这样的分式就是假分式;
这样的分式就是假分式;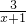 ,
,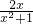 这样的分式就是真分式.类似的,假分式也可以化为带分式(即:整式与真分式和的形式).
这样的分式就是真分式.类似的,假分式也可以化为带分式(即:整式与真分式和的形式).
例如: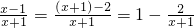 ;
; 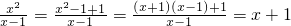 +
+ .
.
(1)将分式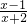 化为带分式;
化为带分式;
(2)若分式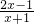 的值为整数,求x的整数值;
的值为整数,求x的整数值;
(3)求函数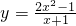 图象上所有横纵坐标均为整数的点的坐标.
图象上所有横纵坐标均为整数的点的坐标.
解:(1)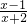 =
= =1-
=1- ;
;
(2)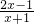 =
= =2-
=2-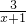 ,
,
∵当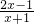 为整数时,
为整数时,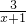 也为整数,
也为整数,
∴x+1可取得的整数值为±1、±3,
∴x的可能整数值为0,-2,2,-4;
(3)y= =
= =2(x-1)+
=2(x-1)+ ,
,
当x,y均为整数时,必有x+1=±1,
解得x=0或-2,
则相应的y值分别为-1或-7,
故所求的坐标为(0,-1)或(-2,-7).
分析:(1)分式分子x-1变形为x+2-3,利用同分母分式减法逆运算法则变形即可得到结果;
(2)将分式分子2x-1变形为2(x+1)-3,利用同分母分式的减法逆运算法则变形后,由分式的值为整数,即可求出x可能的值;
(3)将函数解析式分子变形后,利用同分母分式的加法逆运算法则变形,根据x与y为整数,得出x与y的值,即可确定出所求的坐标.
点评:此题考查了分式的混合运算,分式的值,以及反比例图象上点的坐标特征,分式的加减运算关键是通分,通分的关键是找最简公分母;分式的乘除运算关键是约分,约分的关键是找公因式,约分时,分式的分子分母出现多项式,应将多项式分解因式后再约分.
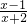 =
= =1-
=1- ;
; (2)
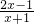 =
= =2-
=2-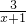 ,
,∵当
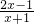 为整数时,
为整数时,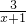 也为整数,
也为整数,∴x+1可取得的整数值为±1、±3,
∴x的可能整数值为0,-2,2,-4;
(3)y=
 =
= =2(x-1)+
=2(x-1)+ ,
,当x,y均为整数时,必有x+1=±1,
解得x=0或-2,
则相应的y值分别为-1或-7,
故所求的坐标为(0,-1)或(-2,-7).
分析:(1)分式分子x-1变形为x+2-3,利用同分母分式减法逆运算法则变形即可得到结果;
(2)将分式分子2x-1变形为2(x+1)-3,利用同分母分式的减法逆运算法则变形后,由分式的值为整数,即可求出x可能的值;
(3)将函数解析式分子变形后,利用同分母分式的加法逆运算法则变形,根据x与y为整数,得出x与y的值,即可确定出所求的坐标.
点评:此题考查了分式的混合运算,分式的值,以及反比例图象上点的坐标特征,分式的加减运算关键是通分,通分的关键是找最简公分母;分式的乘除运算关键是约分,约分的关键是找公因式,约分时,分式的分子分母出现多项式,应将多项式分解因式后再约分.

练习册系列答案
相关题目