ΧβΡΩΡΎ»ί
Έ“Ο«÷ΣΒάΘ§ΦΌΖ÷ ΐΩ…“‘Μ·ΈΣ¥χΖ÷ ΐΘ°άΐ»γΘΚ
=2+
=2
Θ°‘ΎΖ÷ Ϋ÷–Θ§Ε‘”Ύ÷ΜΚ§”–“ΜΗωΉ÷ΡΗΒΡΖ÷ ΫΘ§Β±Ζ÷Ή”ΒΡ¥Έ ΐ¥σ”ΎΜρΒ»”ΎΖ÷ΡΗΒΡ¥Έ ΐ ±Θ§Έ“Ο«≥Τ÷°ΈΣΓΑΦΌΖ÷ ΫΓ±ΘΜΒ±Ζ÷Ή”ΒΡ¥Έ ΐ–Γ”ΎΖ÷ΡΗΒΡ¥Έ ΐ ±Θ§Έ“Ο«≥Τ÷°ΈΣΓΑ’φΖ÷ ΫΓ±Θ°άΐ»γΘΚ
Θ§
’β―υΒΡΖ÷ ΫΨΆ «ΦΌΖ÷ ΫΘΜ
Θ§
’β―υΒΡΖ÷ ΫΨΆ «’φΖ÷ ΫΘ°άύΥΤΒΡΘ§ΦΌΖ÷ Ϋ“≤Ω…“‘Μ·ΈΣ¥χΖ÷ ΫΘ®Φ¥ΘΚ’ϊ Ϋ”κ’φΖ÷ ΫΚΆΒΡ–Έ ΫΘ©Θ°
άΐ»γΘΚ
=
=1-
ΘΜ
=
=
=x+1+
Θ°
Θ®1Θ©ΫΪΖ÷ Ϋ
Μ·ΈΣ¥χΖ÷ ΫΘΜ
Θ®2Θ©»τΖ÷ Ϋ
ΒΡ÷ΒΈΣ’ϊ ΐΘ§«σxΒΡ’ϊ ΐ÷ΒΘΜ
Θ®3Θ©«σΚ· ΐy=
ΆΦœσ…œΥυ”–ΚαΉίΉχ±ξΨυΈΣ’ϊ ΐΒΡΒψΒΡΉχ±ξΘ°
| 8 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| x-1 |
| x+1 |
| x2 |
| x-1 |
| 3 |
| x+1 |
| 2x |
| x2+1 |
άΐ»γΘΚ
| x-1 |
| x+1 |
| (x+1)-2 |
| x+1 |
| 2 |
| x+1 |
| x2 |
| x-1 |
| x2-1+1 |
| x-1 |
| (x+1)(x-1)+1 |
| x-1 |
| 1 |
| x-1 |
Θ®1Θ©ΫΪΖ÷ Ϋ
| x-1 |
| x+2 |
Θ®2Θ©»τΖ÷ Ϋ
| 2x-1 |
| x+1 |
Θ®3Θ©«σΚ· ΐy=
| 2x2-1 |
| x+1 |
Ζ÷ΈωΘΚΘ®1Θ©Ζ÷ ΫΖ÷Ή”x-1±δ–ΈΈΣx+2-3Θ§άϊ”ΟΆ§Ζ÷ΡΗΖ÷ ΫΦθΖ®Ρφ‘ΥΥψΖ®‘ρ±δ–ΈΦ¥Ω…ΒΟΒΫΫαΙϊΘΜ
Θ®2Θ©ΫΪΖ÷ ΫΖ÷Ή”2x-1±δ–ΈΈΣ2Θ®x+1Θ©-3Θ§άϊ”ΟΆ§Ζ÷ΡΗΖ÷ ΫΒΡΦθΖ®Ρφ‘ΥΥψΖ®‘ρ±δ–ΈΚσΘ§”…Ζ÷ ΫΒΡ÷ΒΈΣ’ϊ ΐΘ§Φ¥Ω…«σ≥ωxΩ…ΡήΒΡ÷ΒΘΜ
Θ®3Θ©ΫΪΚ· ΐΫβΈω ΫΖ÷Ή”±δ–ΈΚσΘ§άϊ”ΟΆ§Ζ÷ΡΗΖ÷ ΫΒΡΦ”Ζ®Ρφ‘ΥΥψΖ®‘ρ±δ–ΈΘ§ΗυΨίx”κyΈΣ’ϊ ΐΘ§ΒΟ≥ωx”κyΒΡ÷ΒΘ§Φ¥Ω…»ΖΕ®≥ωΥυ«σΒΡΉχ±ξΘ°
Θ®2Θ©ΫΪΖ÷ ΫΖ÷Ή”2x-1±δ–ΈΈΣ2Θ®x+1Θ©-3Θ§άϊ”ΟΆ§Ζ÷ΡΗΖ÷ ΫΒΡΦθΖ®Ρφ‘ΥΥψΖ®‘ρ±δ–ΈΚσΘ§”…Ζ÷ ΫΒΡ÷ΒΈΣ’ϊ ΐΘ§Φ¥Ω…«σ≥ωxΩ…ΡήΒΡ÷ΒΘΜ
Θ®3Θ©ΫΪΚ· ΐΫβΈω ΫΖ÷Ή”±δ–ΈΚσΘ§άϊ”ΟΆ§Ζ÷ΡΗΖ÷ ΫΒΡΦ”Ζ®Ρφ‘ΥΥψΖ®‘ρ±δ–ΈΘ§ΗυΨίx”κyΈΣ’ϊ ΐΘ§ΒΟ≥ωx”κyΒΡ÷ΒΘ§Φ¥Ω…»ΖΕ®≥ωΥυ«σΒΡΉχ±ξΘ°
Ϋβ¥πΘΚΫβΘΚΘ®1Θ©
=
=1-
ΘΜ
Θ®2Θ©
=
=2-
Θ§
ΓΏΒ±
ΈΣ’ϊ ΐ ±Θ§
“≤ΈΣ’ϊ ΐΘ§
Γύx+1Ω…»ΓΒΟΒΡ’ϊ ΐ÷ΒΈΣΓά1ΓΔΓά3Θ§
ΓύxΒΡΩ…Ρή’ϊ ΐ÷ΒΈΣ0Θ§-2Θ§2Θ§-4ΘΜ
Θ®3Θ©y=
=
=2Θ®x-1Θ©+
Θ§
Β±xΘ§yΨυΈΣ’ϊ ΐ ±Θ§±Ί”–x+1=Γά1Θ§
ΫβΒΟx=0Μρ-2Θ§
‘ρœύ”ΠΒΡy÷ΒΖ÷±πΈΣ-1Μρ-7Θ§
Ι Υυ«σΒΡΉχ±ξΈΣΘ®0Θ§-1Θ©ΜρΘ®-2Θ§-7Θ©Θ°
| x-1 |
| x+2 |
| (x+2)-3 |
| x+2 |
| 3 |
| x+2 |
Θ®2Θ©
| 2x-1 |
| x+1 |
| 2(x+1)-3 |
| x+1 |
| 3 |
| x+1 |
ΓΏΒ±
| 2x-1 |
| x+1 |
| 3 |
| x+1 |
Γύx+1Ω…»ΓΒΟΒΡ’ϊ ΐ÷ΒΈΣΓά1ΓΔΓά3Θ§
ΓύxΒΡΩ…Ρή’ϊ ΐ÷ΒΈΣ0Θ§-2Θ§2Θ§-4ΘΜ
Θ®3Θ©y=
| 2x2-1 |
| x+1 |
| 2(x2-1)+1 |
| x+1 |
| 1 |
| x+1 |
Β±xΘ§yΨυΈΣ’ϊ ΐ ±Θ§±Ί”–x+1=Γά1Θ§
ΫβΒΟx=0Μρ-2Θ§
‘ρœύ”ΠΒΡy÷ΒΖ÷±πΈΣ-1Μρ-7Θ§
Ι Υυ«σΒΡΉχ±ξΈΣΘ®0Θ§-1Θ©ΜρΘ®-2Θ§-7Θ©Θ°
ΒψΤάΘΚ¥ΥΧβΩΦ≤ιΝΥΖ÷ ΫΒΡΜλΚœ‘ΥΥψΘ§Ζ÷ ΫΒΡ÷ΒΘ§“‘ΦΑΖ¥±»άΐΆΦœσ…œΒψΒΡΉχ±ξΧΊ’ςΘ§Ζ÷ ΫΒΡΦ”Φθ‘ΥΥψΙΊΦϋ «Ά®Ζ÷Θ§Ά®Ζ÷ΒΡΙΊΦϋ «’“ΉνΦρΙΪΖ÷ΡΗΘΜΖ÷ ΫΒΡ≥Υ≥ΐ‘ΥΥψΙΊΦϋ «‘ΦΖ÷Θ§‘ΦΖ÷ΒΡΙΊΦϋ «’“ΙΪ“ρ ΫΘ§‘ΦΖ÷ ±Θ§Ζ÷ ΫΒΡΖ÷Ή”Ζ÷ΡΗ≥ωœ÷Εύœν ΫΘ§”ΠΫΪΕύœν ΫΖ÷Ϋβ“ρ ΫΚσ‘Ό‘ΦΖ÷Θ°

ΝΖœΑ≤αœΒΝ–¥πΑΗ
 Ά§≤ΫΝΖœΑΚ”Ρœ¥σ―ß≥ωΑφ…γœΒΝ–¥πΑΗ
Ά§≤ΫΝΖœΑΚ”Ρœ¥σ―ß≥ωΑφ…γœΒΝ–¥πΑΗ Ά§≤ΫΝΖœΑΈςΡœ ΠΖΕ¥σ―ß≥ωΑφ…γœΒΝ–¥πΑΗ
Ά§≤ΫΝΖœΑΈςΡœ ΠΖΕ¥σ―ß≥ωΑφ…γœΒΝ–¥πΑΗ ≤Ι≥δœΑΧβΫ≠Υ’œΒΝ–¥πΑΗ
≤Ι≥δœΑΧβΫ≠Υ’œΒΝ–¥πΑΗ ―ßΝΖΩλ≥ΒΒάΩΎΥψ–ΡΥψΥΌΥψΧλΧλΝΖœΒΝ–¥πΑΗ
―ßΝΖΩλ≥ΒΒάΩΎΥψ–ΡΥψΥΌΥψΧλΧλΝΖœΒΝ–¥πΑΗ
œύΙΊΧβΡΩ
 =
=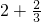 =
=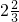 Θ°‘ΎΖ÷ Ϋ÷–Θ§Ε‘”Ύ÷ΜΚ§”–“ΜΗωΉ÷ΡΗΒΡΖ÷ ΫΘ§Β±Ζ÷Ή”ΒΡ¥Έ ΐ¥σ”ΎΜρΒ»”ΎΖ÷ΡΗΒΡ¥Έ ΐ ±Θ§Έ“Ο«≥Τ÷°ΈΣΓΑΦΌΖ÷ ΫΓ±ΘΜΒ±Ζ÷Ή”ΒΡ¥Έ ΐ–Γ”ΎΖ÷ΡΗΒΡ¥Έ ΐ ±Θ§Έ“Ο«≥Τ÷°ΈΣΓΑ’φΖ÷ ΫΓ±Θ°άΐ»γΘΚ
Θ°‘ΎΖ÷ Ϋ÷–Θ§Ε‘”Ύ÷ΜΚ§”–“ΜΗωΉ÷ΡΗΒΡΖ÷ ΫΘ§Β±Ζ÷Ή”ΒΡ¥Έ ΐ¥σ”ΎΜρΒ»”ΎΖ÷ΡΗΒΡ¥Έ ΐ ±Θ§Έ“Ο«≥Τ÷°ΈΣΓΑΦΌΖ÷ ΫΓ±ΘΜΒ±Ζ÷Ή”ΒΡ¥Έ ΐ–Γ”ΎΖ÷ΡΗΒΡ¥Έ ΐ ±Θ§Έ“Ο«≥Τ÷°ΈΣΓΑ’φΖ÷ ΫΓ±Θ°άΐ»γΘΚ Θ§
Θ§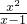 ’β―υΒΡΖ÷ ΫΨΆ «ΦΌΖ÷ ΫΘΜ
’β―υΒΡΖ÷ ΫΨΆ «ΦΌΖ÷ ΫΘΜ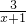 Θ§
Θ§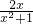 ’β―υΒΡΖ÷ ΫΨΆ «’φΖ÷ ΫΘ°άύΥΤΒΡΘ§ΦΌΖ÷ Ϋ“≤Ω…“‘Μ·ΈΣ¥χΖ÷ ΫΘ®Φ¥ΘΚ’ϊ Ϋ”κ’φΖ÷ ΫΚΆΒΡ–Έ ΫΘ©Θ°
’β―υΒΡΖ÷ ΫΨΆ «’φΖ÷ ΫΘ°άύΥΤΒΡΘ§ΦΌΖ÷ Ϋ“≤Ω…“‘Μ·ΈΣ¥χΖ÷ ΫΘ®Φ¥ΘΚ’ϊ Ϋ”κ’φΖ÷ ΫΚΆΒΡ–Έ ΫΘ©Θ°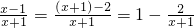 ΘΜ
ΘΜ 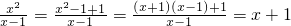 +
+ Θ°
Θ°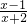 Μ·ΈΣ¥χΖ÷ ΫΘΜ
Μ·ΈΣ¥χΖ÷ ΫΘΜ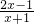 ΒΡ÷ΒΈΣ’ϊ ΐΘ§«σxΒΡ’ϊ ΐ÷ΒΘΜ
ΒΡ÷ΒΈΣ’ϊ ΐΘ§«σxΒΡ’ϊ ΐ÷ΒΘΜ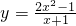 ΆΦœσ…œΥυ”–ΚαΉίΉχ±ξΨυΈΣ’ϊ ΐΒΡΒψΒΡΉχ±ξΘ°
ΆΦœσ…œΥυ”–ΚαΉίΉχ±ξΨυΈΣ’ϊ ΐΒΡΒψΒΡΉχ±ξΘ°