题目内容
 已知,二次函数的解析式为y=-x2+2x+3.
已知,二次函数的解析式为y=-x2+2x+3.(1)它与x轴的交点的坐标为
(3,0)(-1,0)
(3,0)(-1,0)
,顶点坐标为(1,4)
(1,4)
;(2)在给定的坐标系中画出这个二次函数的图象,并求出抛物线与坐标轴的交点所组成的三角形的面积;
(3)根据图象直接写出抛物线在-1<x<2范围内,函数值y的取值范围是
0<y≤4
0<y≤4
.分析:(1)设y=0,求出x的值即它与x轴的交点的横坐标;把函数的表达式配方即可求出顶点坐标;
(2)由(1)可知抛物线和x轴的交点坐标、顶点坐标,再求出抛物线和y轴的交点即可确定抛物线的位置,根据三角形的面积公式抛物线与坐标轴的交点所组成的三角形的面积;
(3)由函数的图象可知抛物线在-1<x<2范围内,对应函数值y的取值范围.
(2)由(1)可知抛物线和x轴的交点坐标、顶点坐标,再求出抛物线和y轴的交点即可确定抛物线的位置,根据三角形的面积公式抛物线与坐标轴的交点所组成的三角形的面积;
(3)由函数的图象可知抛物线在-1<x<2范围内,对应函数值y的取值范围.
解答: 解:(1)设y=0,即0=-x2+2x+3,解得:x=3或-1,
解:(1)设y=0,即0=-x2+2x+3,解得:x=3或-1,
∴它与x轴的交点的坐标为 (3,0)(-1,0),
∵y=-x2+2x+3=-(x-1)2+4,
∴顶点坐标为(1,4);
故答案为:(3,0)(-1,0);(1,4);
(2)函数图象如图所示:
三角形的面积=
×3×4=6;
(3)由函数图形可知:当-1<x<2,函数值y的取值范围是0<y≤4,
故答案为0<y≤4.
 解:(1)设y=0,即0=-x2+2x+3,解得:x=3或-1,
解:(1)设y=0,即0=-x2+2x+3,解得:x=3或-1,∴它与x轴的交点的坐标为 (3,0)(-1,0),
∵y=-x2+2x+3=-(x-1)2+4,
∴顶点坐标为(1,4);
故答案为:(3,0)(-1,0);(1,4);
(2)函数图象如图所示:
三角形的面积=
| 1 |
| 2 |
(3)由函数图形可知:当-1<x<2,函数值y的取值范围是0<y≤4,
故答案为0<y≤4.
点评:本题考查了抛物线的开口方向、对称轴、顶点坐标、最值与抛物线解析式的关系,抛物线的顶点式:y=a(x-h)2+k,顶点坐标为(h,k),对称轴x=h.同时考查了用抛物线与x轴的交点坐标,判断函数值的符号的方法.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 已知,二次函数的解析式y1=-x2+2x+3.
已知,二次函数的解析式y1=-x2+2x+3.
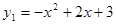 。
。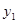 随x的增大而增大;
随x的增大而增大;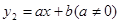 的图象与该二次图象交于A(
的图象与该二次图象交于A(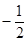 ,
, ),B(2,n)两点,结合图象直接写出当x取何值时
),B(2,n)两点,结合图象直接写出当x取何值时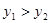 ?
?