题目内容
 已知,二次函数的解析式y1=-x2+2x+3.
已知,二次函数的解析式y1=-x2+2x+3.(1)求这个二次函数的顶点坐标;
(2)求这个二次函数图象与x轴的交点坐标;
(3)当x
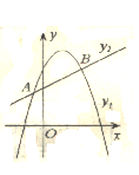
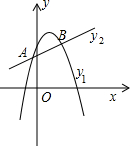
(4)如图,若直线y2=ax+b(a≠0)的图象与该二次图象交于A(-
| 1 | 2 |
分析:(1)运用配方法可求出二次函数的顶点坐标,
(2)求图象与与x轴的交点,即求y=0时x的值,
(3)根据对称轴两侧增减性不同,求出对称轴,结合开口方向可求出,
(4)根据两函数交点,结合图象可看出.
(2)求图象与与x轴的交点,即求y=0时x的值,
(3)根据对称轴两侧增减性不同,求出对称轴,结合开口方向可求出,
(4)根据两函数交点,结合图象可看出.
解答:解:(1)∵y1=-(x2-2x+1)+4=-(x-1)2+4,
∴图象的顶点坐标为(1,4).
(2)令y=0,则-x2+2x+3=0,
解得:x1=-1,x2=3.
∴图象与x轴的交点坐标分别为(-1,0)、(3,0).
(3)x<1.
(4)y1=-x2+2x+3,结合图象可得到.
y1>y2,-
<x<2.
∴图象的顶点坐标为(1,4).
(2)令y=0,则-x2+2x+3=0,
解得:x1=-1,x2=3.
∴图象与x轴的交点坐标分别为(-1,0)、(3,0).
(3)x<1.
(4)y1=-x2+2x+3,结合图象可得到.
y1>y2,-
| 1 |
| 2 |
点评:此题主要考查了二次函数顶点坐标的求法,二次函数与x轴的交点坐标求法,以及结合图象判断函数的大小问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知,二次函数的解析式为y=-x2+2x+3.
已知,二次函数的解析式为y=-x2+2x+3.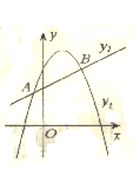
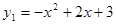 。
。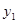 随x的增大而增大;
随x的增大而增大;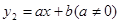 的图象与该二次图象交于A(
的图象与该二次图象交于A(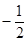 ,
, ),B(2,n)两点,结合图象直接写出当x取何值时
),B(2,n)两点,结合图象直接写出当x取何值时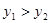 ?
?