Question

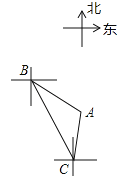
【题目】在平面直角坐标系中，三角形ABC的三个顶点的位置如图所示，点A′的坐标是（﹣2，2），现将三角形ABC平移，使点A变换为点A′，点B′、C′分别是B、C的对应点．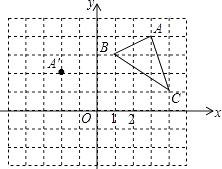

（1）请画出平移后的三角形A′B′C′（不写画法），并写出点B′、C′的坐标；
（2）求三角形ABC的面积．

Answer 1

【答案】
（1）解：如图所示，△A′B′C′为所求三角形，且，B′（﹣4，1），C′（﹣1，﹣1）；

（2）解：三角形ABC的面积S=3×3﹣ ×2×1﹣ ×2×3﹣ ×1×3=9﹣1﹣3﹣1.5=3.5

【解析】①观察图形，结合A的位置变化，根据网格结构找出点B、C平移后的位置，然后顺次连接，即可画出平移后的三角形A′B′C′；
再结合网格特点，根据平面直角坐标系的相关知识，直接写出点B′、C′的坐标即可；
②根据点A及点A′的坐标，可得出平移规律，继而得出点P平移后的对应点P′的坐标.

【考点精析】根据题目的已知条件，利用坐标与图形变化-平移的相关知识可以得到问题的答案，需要掌握新图形的每一点，都是由原图形中的某一点移动后得到的，这两个点是对应点；连接各组对应点的线段平行且相等．