题目内容
【题目】如图,在菱形ABCD中,AB=10,AC=16,点M是对角线AC上的一个动点,过点M作PQ⊥AC交AB于点P,交AD于点Q,将△APQ沿PQ折叠,点A落在点E处,当△BCE是等腰三角形时,AP的长为 
【答案】![]() 或
或 ![]()
【解析】解:连接BD交AC于O,
∵四边形ABCD是菱形,
∴AC⊥BD,
∵PQ⊥AC,AO= ![]() AC=8,
AC=8,
∴PQ∥BD,
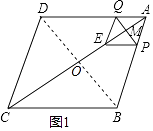
∴△AMP∽△AOB,①当CE=CB时,如图1,则CE=10,AE=6,AM=3,
∵△AMP∽△AOB,
∴ ![]() =
= ![]() ,
,
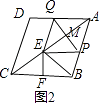
∴AP= ![]() ;②当BE=EC时,如图2,点E是BC的垂直平分线与AC的交点,则CF=5,∵△CEF∽△CBO,
;②当BE=EC时,如图2,点E是BC的垂直平分线与AC的交点,则CF=5,∵△CEF∽△CBO,
∴CE= ![]() =
= ![]() ,∴AE=16﹣
,∴AE=16﹣ ![]() =
= ![]() ,
,
∴AM= ![]() ,
,
∴AP= ![]() =
= ![]() ;③当BC=BE时,E与A重合;
;③当BC=BE时,E与A重合;
综上所述:当△BCE是等腰三角形时,AP的长为 ![]() 或
或 ![]() .
.
所以答案是: ![]() 或
或 ![]() .
.
【考点精析】利用等腰三角形的性质和菱形的性质对题目进行判断即可得到答案,需要熟知等腰三角形的两个底角相等(简称:等边对等角);菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.

【题目】某出版社出版适合中学生阅读的科普读物,该读物首次出版印刷的印数不少于5000册时,投入的成本与印数间的相应数据如下表:
印数x(册) | 5000 | 8000 | 11000 | 14000 | … |
成本y(元) | 28500 | 36000 | 43500 | 51000 | … |
(1)通过对上表中数据的探究,你发现这种读物的投入成本y(元)是印数x(册)的正比例函数?还是一次函数?并求出这个函数的表达式(不要求写出x的取值范围);
(2)如果出版社投入成本60000元,那么能印该读物多少册?


