题目内容
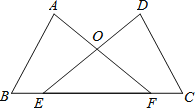
【题目】（1）如图，点E.F在BC上，BE=CF，AB=DC，∠B=∠C.求证：∠A=∠D.
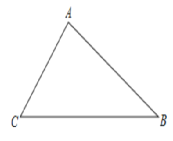
（2）已知如图,在△ABC中,∠B=30°,∠C=45°,ABAC=2
，求BC的长.
【答案】（1）见解析；（2）1+
.
【解析】
（1）先根据等式性质证明BF=EC，再利用SAS证明△ABF≌△DCE即可．
（2）过A作AD⊥BC于D，设AD=x，求出AB=2x，AC=
x，代入AB-AC=2-，求出x，即可求出BC．
（1）证明：∵BE=FC，
∴BE+EF=FC+EF，
即BF=EC，
在△ABF和△DCE中，
，
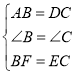∴△ABF≌△DCE(SAS)，
∴∠A=∠D.
（2）过A作AD⊥BC于D，设AD=x，
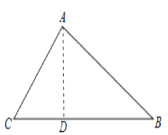
∠ADC=∠ADB=90°，
∵∠C=45°,∠B=30°，
∴AB=2x,∠DAC=45°=∠C，
∴CD=AD=x，
在Rt△CDA中,由勾股定理得：AC=x，
在Rt△BDA中,由勾股定理得：BD=x，
∵ABAC=2，
∴2xx=2，
∴x=1，
∴BC=CD+BD=1+.
练习册系列答案
相关题目
【题目】小明和小亮玩扑克牌游戏，小明背对小亮，让小亮按下列四个步骤操作：
第一步：分发左、中、右三堆牌，每堆牌都为
张，且
；
第二步：从左边一堆拿出两张，放入中间一堆；
第三步：从右边一堆拿出五张，放入中间一堆
第四步：左边一堆有几张牌，就从中间一堆拿几张牌放入左边一堆．
（1）填写下表中的空格：
步骤 | 左边一堆牌的张数 | 中间一堆牌的张数 | 右边一堆牌的张数 |
第一步后 |
|
|
|
第二步后 |
|
| |
第三步后 |
|
| |
第四步后 |
|
（2）如若第四步完成后，中间一堆牌的张数的2倍恰好是右边一堆牌的张数的3倍，试求第一步后，每堆牌各有多少张？
