题目内容
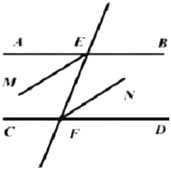
【题目】如图，直线
，
相交于点
，
平分
，
于点，
，请补全图形，并求出
的度数.
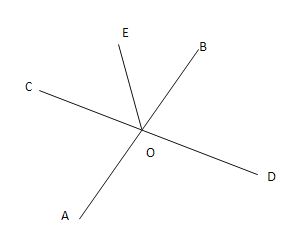
【答案】图见解析；
=135°或45°
【解析】
根据OF与CD的相对位置分类讨论：①若OF在CD上方时，根据题意，可设：
，再根据角平分线的定义可得：∠BOC=2
，然后根据平角的定义列出方程，即可求出x，从而求出∠AOC，再根据垂直的定义即可求出的度数；②若OF在CD下方时，原理同上.
解：①若OF在CD上方时，如图所示，
∵
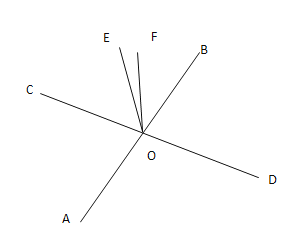
设
∵
平分
∴∠BOC=2
∵∠BOC＋∠BOD=180°
∴
解得：
∴∠AOC=∠BOD=2×22.5°=45°
∵
∴∠COF=90°
∴∠AOF=∠AOC＋∠COF=135°
②若OF在CD下方时，如图所示，
∵
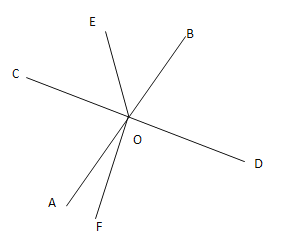
设
∵平分
∴∠BOC=2
∵∠BOC＋∠BOD=180°
∴
解得：
∴∠AOC=∠BOD=2×22.5°=45°
∵
∴∠COF=90°
∴∠AOF=∠COF－∠AOC=45°
综上所述：=135°或45°.
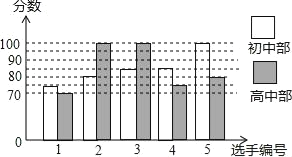
阅读快车系列答案【题目】某学校举行“中国梦，我的梦”演讲比赛，初、高中部根据初赛成绩，各选出5名选手组成代表队决赛，初、高中部代表队的选手决赛成绩如图所示：
（1）根据图示填写表格：
平均数（分） | 中位数（分） | 众数（分） | |
初中代表队 | 85 |
| 85 |
高中代表队 |
| 80 |
|
（2）结合两队成绩的平均数和中位数，分析哪个队的决赛成绩较好．
【题目】某区举行“中华诵
经典诵读”大赛，小学、中学组根据初赛成绩，各选出5名选手组成小学代表队和中学代表队参加市级决赛，两个代表队各选出的5名选手的决赛成绩分别绘制成下列两个统计图
根据以上信息，整理分析数据如下：
平均数（分 | 中位数（分 | 众数（分 | |
小学组 | 85 |
| 100 |
中学组 |
| 85 |
|
（1）写出表格中
，
，
的值：
，
，
．
（2）结合两队成绩的平均数和中位数进行分析，哪个队的决赛成绩较好？
（3）计算两队决赛成绩的方差，并判断哪一个代表队选手成绩较稳定．
