题目内容
请阅读下列材料?:
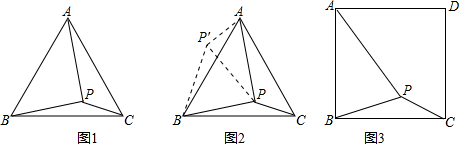
问题:如图1,在等边三角形ABC内有一点P,且PA=2,PB=
,PC=1.求∠BPC度数的大小和等边三角形ABC的边长.
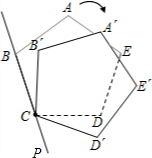
李明同学的思路是:将△BPC绕点B顺时针旋转60°,画出旋转后的图形(如图2).连接PP′,可得△P′PB是等边三角形(可证),而△PP′A又是直角三角形(由勾股定理的逆定理可证).所以∠AP′B=150°,而∠BPC=∠AP′B=150°.进而把AB放在Rt△APB(可证得)中,用勾股定理求出等边△ABC的边长为
.问题得到解决.?
[思路分析]首先仔细阅读材料,问题中小明的做法总结起来就是通过旋转固定的角度将已知条件放在同一个(组)图形中进行研究.旋转60度以后BP就成了BP′,PC成了P′A,借助等量关系BP′=PP′,于是△APP′就可以计算了.
解决问题:
请你参考李明同学旋转的思路,探究并解决下列问题:
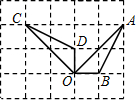
如图3,在正方形ABCD内有一点P,且PA=
,BP=
,PC=1.求∠BPC度数的大小和正方形ABCD的边长.
问题:如图1,在等边三角形ABC内有一点P,且PA=2,PB=
| 3 |
李明同学的思路是:将△BPC绕点B顺时针旋转60°,画出旋转后的图形(如图2).连接PP′,可得△P′PB是等边三角形(可证),而△PP′A又是直角三角形(由勾股定理的逆定理可证).所以∠AP′B=150°,而∠BPC=∠AP′B=150°.进而把AB放在Rt△APB(可证得)中,用勾股定理求出等边△ABC的边长为
| 7 |
[思路分析]首先仔细阅读材料,问题中小明的做法总结起来就是通过旋转固定的角度将已知条件放在同一个(组)图形中进行研究.旋转60度以后BP就成了BP′,PC成了P′A,借助等量关系BP′=PP′,于是△APP′就可以计算了.
解决问题:
请你参考李明同学旋转的思路,探究并解决下列问题:
如图3,在正方形ABCD内有一点P,且PA=
| 5 |
| 2 |

如图3,
将△BPC绕点B逆时针旋转90°,得△BP′A,
则△BPC≌△BP′A.
∴AP′=PC=1,BP=BP′=
.
连结PP′,
在Rt△BP′P中,
∵BP=BP′=
,∠PBP′=90°,
∴PP′=2,∠BP′P=45°.
在△AP′P中,AP′=1,PP′=2,AP=
,
∵12+22=(
)2,
即AP′2+PP′2=AP2.
∴△AP′P是直角三角形,即∠AP′P=90°.
∴∠AP′B=135°.
∴∠BPC=∠AP′B=135°.
如图3,过点B作BE⊥AP′交AP′的延长线于点E.
∴∠EP′B=45°.∴EP′=BE=1.∴AE=2.
∴在Rt△ABE中,由勾股定理,得AB=
.
∴∠BPC=135°,正方形边长为
.

将△BPC绕点B逆时针旋转90°,得△BP′A,
则△BPC≌△BP′A.
∴AP′=PC=1,BP=BP′=
| 2 |
连结PP′,
在Rt△BP′P中,
∵BP=BP′=
| 2 |
∴PP′=2,∠BP′P=45°.
在△AP′P中,AP′=1,PP′=2,AP=
| 5 |
∵12+22=(
| 5 |
即AP′2+PP′2=AP2.
∴△AP′P是直角三角形,即∠AP′P=90°.
∴∠AP′B=135°.
∴∠BPC=∠AP′B=135°.
如图3,过点B作BE⊥AP′交AP′的延长线于点E.
∴∠EP′B=45°.∴EP′=BE=1.∴AE=2.
∴在Rt△ABE中,由勾股定理,得AB=
| 5 |
∴∠BPC=135°,正方形边长为
| 5 |


练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目