题目内容
【题目】如图,![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 绕点
绕点![]() 旋转,
旋转,![]() 分别与边
分别与边![]() 交于
交于![]() 两点
两点
⑴求证:![]() 是等腰直角三角形;
是等腰直角三角形;
⑵求证:![]() ;
;
⑶若![]() 的长为16,求四边形
的长为16,求四边形![]() 的面积.
的面积.
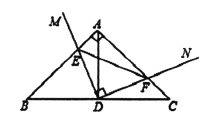
【答案】(1)证明见解析;(2)证明见解析;(3)32.
【解析】
(1)根据等腰直角三角形的性质,得到∠C=∠BAD=45°,AD=BD=CD,然后利用ASA证明三角形全等,即可得到结论;
(2)由(1)可知,AE=CF,然后得到结论成立;
(3)由(1)可知,利用全等三角形面积相等,即可求出四边形的面积.
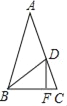
(1)证明:∵Rt△ABC中,AB=AC,点D为BC中点,
∴∠C=∠BAD=45°,AD=BD=CD,
∵∠MDN=90°,
∴∠ADE+∠ADF=∠ADF+∠CDF=90°,
∴∠ADE=∠CDF.
在△AED与△CFD中,
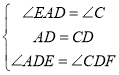 ,
,
∴△AED≌△CFD(ASA),
∴ED=FD.;
(2)由(1)得,△AED≌△CFD,
∴AE=CF,
∴BE+CF=BE+AE=AB=AC;
(3)∵△AED≌△CFD,
∴S四边形AEDF=S△ADE+ S△ADF
=S△CDF+ S△ADF = S△ADC
= ![]() AD2.
AD2.
由已知可得,AD=BD=CD=8
∴S四边形AEDF== ![]() AD2=
AD2=![]() =32.
=32.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目