题目内容
【题目】如图，AB是⊙O的直径，弦CD⊥AB于点P，CD=10cm，AP：PB=1：5，那么⊙O的半径是（ ）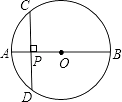 
A.5 
cm
B.4 
cm
C.3 
cm
D.2 
cm
【答案】C
【解析】解：设AP=x，则PB=5x，那么⊙O的半径是 
（x+5x）=3x∵弦CD⊥AB于点P，CD=10cm
∴PC=PD= CD= ×10=5cm
由相交弦定理得CPPD=APPB
即5×5=x5x
解得x= 
或x=﹣ （舍去）
故⊙O的半径是3x=3 cm，
故选C．
【考点精析】利用勾股定理的概念和垂径定理对题目进行判断即可得到答案，需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；垂径定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧．
练习册系列答案
相关题目
