题目内容
【题目】如图,在△ABC中,AB=13,BC=14,AC=15,点D在AC上(可与点A,C重合),分别过点A、C作直线BD的垂线,垂足为E,F,则AE+CF的最大值为_____,最小值为_____.
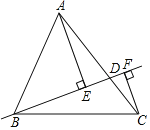
【答案】15 12
【解析】
设AE=m,CF=n,则m+n=y,用m、n及x表示出△ABD及△CBD的面积,根据S△ABC=S△ABD+S△CBD即可得到m+n关于x的反比例函数关系式.根据垂直线段最短的性质,当BD⊥AC时,x最小,由面积公式可求得;因为AB=13,BC=14,所以当BD=BC=14时,x最大.从而根据反比例函数的性质求出y的最大值和最小值.
设BD=x,AE+CF=y,AE=m,CF=n,则m+n=y,
∵由三角形面积公式,得![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() .
.
∵△ABC中AC边上的高为![]() ,
,
∴x的取值范围为![]() .
.
∵m+n随x的增大而减小,
∴当![]() 时,y的最大值为15,当x=14时,y的最小值为12.
时,y的最大值为15,当x=14时,y的最小值为12.
故答案为:15,12.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目