��Ŀ����
����Ŀ����̽�����֣�
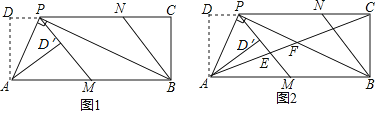
![]() ��ͼ1����һ��ֱ��������ֽƬ��
��ͼ1����һ��ֱ��������ֽƬ��![]() ��С������м���һ����
��С������м���һ����![]() Ϊ�ڽ���������ľ��Σ�������β������֣���������λ��DE��EF����ʱ�����õľ��ε������������ͨ��֤����֤������ȷ�ԣ����ó������ε���������ԭ����������ı�ֵΪ______��
Ϊ�ڽ���������ľ��Σ�������β������֣���������λ��DE��EF����ʱ�����õľ��ε������������ͨ��֤����֤������ȷ�ԣ����ó������ε���������ԭ����������ı�ֵΪ______��
����չӦ�ã�
![]() ��ͼ2����
��ͼ2����![]() �У�
�У�![]() ��BC���ϵĸ�
��BC���ϵĸ�![]() ������PQMN�Ķ���P��N�ֱ��ڱ�AB��AC�ϣ�����Q��M�ڱ�BC�ϣ��������PQMN��������ֵ
������PQMN�Ķ���P��N�ֱ��ڱ�AB��AC�ϣ�����Q��M�ڱ�BC�ϣ��������PQMN��������ֵ![]() �ú�a��h�Ĵ���ʽ��ʾ
�ú�a��h�Ĵ���ʽ��ʾ![]() ��
��
�����Ӧ�ã�
![]() ��ͼ3����һ����ȱ�Ǿ�����ABCDE��
��ͼ3����һ����ȱ�Ǿ�����ABCDE��![]() ��
��![]() ��
��![]() ��
��![]() ��С�����м�����һ��������ľ���
��С�����м�����һ��������ľ���![]() Ϊ���������ε��ڽ�
Ϊ���������ε��ڽ�![]() ��ֱ��д���þ��ε������
��ֱ��д���þ��ε������
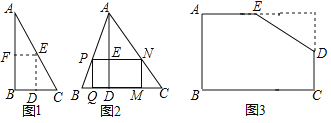
���𰸡���1��![]() ����2��
����2��![]() ��3����
��3����![]() ʱ������BGPH�����ȡ�����ֵ�����ֵΪ567��
ʱ������BGPH�����ȡ�����ֵ�����ֵΪ567��
��������
��1������λ��֪EF=![]() BC��ED=
BC��ED=![]() AB����
AB����![]() �ɵã�
�ɵã�
��2������APN�ס�ABC֪![]() ���ɵ�PN=a-
���ɵ�PN=a-![]() ����PQ=x����S����PQMN=PQPN=
����PQ=x����S����PQMN=PQPN=![]() ���ݴ˿ɵã�
���ݴ˿ɵã�
��3�����ͼ�ι�DE�ϵĵ�P��PG��BC�ڵ�G���ӳ�GP��AE�ӳ����ڵ�I������P��PH��AB����PG=x��֪PI=28-x������EIP�ס�EKD֪![]() ���ݴ����EI=
���ݴ����EI=![]() ��PH=
��PH=![]() ���ٸ��ݾ���BGPH�����S=
���ٸ��ݾ���BGPH�����S=![]() �ɵô𰸣�
�ɵô𰸣�
�⣺![]() ��EDΪ
��EDΪ![]() ��λ�ߣ�
��λ�ߣ�
![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��![]() ��
��
![]() �ı���FEDB�Ǿ��Σ�
�ı���FEDB�Ǿ��Σ�
��![]() ��
��
�ʴ�Ϊ��![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��
![]() ���ɵ�
���ɵ�![]() ��
��
��![]() ����
����![]() ��
��
![]() ��
��![]() ʱ��
ʱ��![]() ���ֵΪ
���ֵΪ![]() ��
��
![]() ��ͼ����DE�ϵĵ�P��
��ͼ����DE�ϵĵ�P��![]() �ڵ�G���ӳ�GP��AE�ӳ����ڵ�I������P��
�ڵ�G���ӳ�GP��AE�ӳ����ڵ�I������P��![]() �ڵ�H��
�ڵ�H��
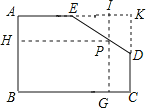
���ı���AHPI���ı���BGPH��Ϊ���Σ�
��![]() ����
����![]() ��
��
![]() ��
��![]() ��
��![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
��![]() ��
��![]() ֪
֪![]() ��
��
��![]() ����
����![]() ��
��
![]() ��
��
�����BGPH�����![]() ��
��
![]() ��
��![]() ʱ������BGPH�����ȡ�����ֵ�����ֵΪ567��
ʱ������BGPH�����ȡ�����ֵ�����ֵΪ567��

 ����ȫ���ִʾ��ƪ��ϵ�д�
����ȫ���ִʾ��ƪ��ϵ�д� �����߿����ϵ�д�
�����߿����ϵ�д�