Question

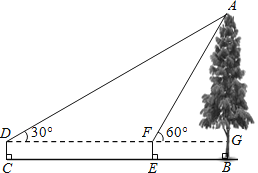
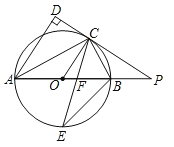
【题目】如图，王华同学在晚上由路灯AC走向路灯BD，当他走到点P时，发现身后他影子的顶部刚好接触到路灯AC的底部，当他向前再步行12m到达Q点时，发现身前他影子的顶部刚好接触到路灯BD的底部．已知王华同学的身高是1.6m，两个路灯的高度都是9.6m．

（1）求两个路灯之间的距离；

（2）当王华同学走到路灯BD处时，他在路灯AC下的影子长是多少？

Answer 1

【答案】（1）两个路灯之间的距离为18米（2）当王华同学走到路灯BD处时，他在路灯AC下的影子长是3.6米

【解析】试题分析：

依题意得到AP=BQ,设AP=BQ=xm，则AB=（2x+12）m，易证得△APM∽△ABD，∴，再由它可以求出x，进而求出AB；
(2)首先要作出此时王华的影子：如图，

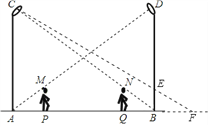
设王华走到路灯BD处头的顶部为E，连接CE并延长交AB的延长线于点F，则BF即为此时他在路灯AC的影子，容易知道△EBF∽△CAF，再利用它们对应边成比例求出现在的影子.

解：

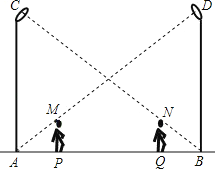
（1）由对称性可知AP=BQ，设AP=BQ=xm，

∵MP∥BD∴△APM∽△ABD，

∴，

∴ ，

解得x=3（m），

检验：当x=3时，2x+12=2×3+12=18≠0，

∴x=3是原方程的根，并且符合题意，

∴AB=2x+12=2×3+12=18（m），

答：两个路灯之间的距离为18米．

（2）如图，设王华走到路灯BD处头的顶部为E，连接CE并延长交AB的延长线于点F，则BF即为此时他在路灯AC的影子长，

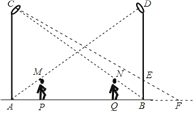
设BF=ym，

∵BE∥AC

∴△EBF∽△CAF

∴ ，即 ，

解得y=3.6（m），

检验当y=3.6时，y+18=3.6+18=21.6≠0，

∴y=3.6是分式方程的解.

答：当王华同学走到路灯BD处时，他在路灯AC下的影子长是3.6米．