题目内容
在平面直角坐标系内存在⊙A,A(b,0),⊙A交x轴于O(0,0)、B(2b,0),在y轴上存在一动点C(C不与原点O重合),直线l始终过A、C,直线l交⊙A于E、F,在半圆EF上存在一点动点D且D不与E、F重合,则S△DEA的最大值为( )
A、
| ||
B、
| ||
C、
| ||
| D、无法判断 |
分析:计算△DEA的面积,关键是确定底和高,在△DEA中,EA是半径,EA=|b|,点D在半圆EF上运动,点D与AE的距离最大值是|b|,故S△DEA的最大值为:
×|b|×|b|=
.
| 1 |
| 2 |
| b2 |
| 2 |
解答: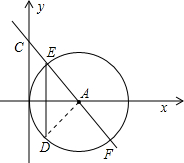 解:∵在△DEA中,当D运动于DA⊥AE时,此时DA作为高是最大的,DA=|b|
解:∵在△DEA中,当D运动于DA⊥AE时,此时DA作为高是最大的,DA=|b|
∵EA=|b|,
∴S△DEA的最大值为:
×|b|×|b|=
.
故选A
 解:∵在△DEA中,当D运动于DA⊥AE时,此时DA作为高是最大的,DA=|b|
解:∵在△DEA中,当D运动于DA⊥AE时,此时DA作为高是最大的,DA=|b|∵EA=|b|,
∴S△DEA的最大值为:
| 1 |
| 2 |
| b2 |
| 2 |
故选A
点评:本题考查了三角形面积的求法,要合理地确定底和高,底一定时,高最大,面积就最大.

练习册系列答案
相关题目
 标为(3,2),B点坐标为(1,0).
标为(3,2),B点坐标为(1,0).
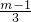 x2+(m-2)x+4m-7与x轴交于A、B 两点(点A在点B的左侧),与y轴交于点C,P是这条抛物线上的一点(点P不在坐标轴上),且点P关于直线BC的对称点在x轴上,D(0,3)是y轴上的一点.
x2+(m-2)x+4m-7与x轴交于A、B 两点(点A在点B的左侧),与y轴交于点C,P是这条抛物线上的一点(点P不在坐标轴上),且点P关于直线BC的对称点在x轴上,D(0,3)是y轴上的一点.
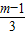 x2+(m-2)x+4m-7与x轴交于A、B 两点(点A在点B的左侧),与y轴交于点C,P是这条抛物线上的一点(点P不在坐标轴上),且点P关于直线BC的对称点在x轴上,D(0,3)是y轴上的一点.
x2+(m-2)x+4m-7与x轴交于A、B 两点(点A在点B的左侧),与y轴交于点C,P是这条抛物线上的一点(点P不在坐标轴上),且点P关于直线BC的对称点在x轴上,D(0,3)是y轴上的一点.