题目内容
如图,将△ABC放在平面直角坐标系中,使B、C在X轴正半轴上,若AB=AC.且A点坐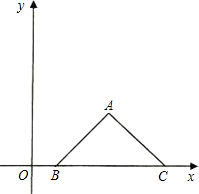 标为(3,2),B点坐标为(1,0).
标为(3,2),B点坐标为(1,0).(1)求边AC所在直线的解析式;
(2)若坐标平面内存在三角形与△ABC全等且有一条公共边,请写出这些三角形未知顶点的坐标.
分析:(1)先根据AB=AC求出C点的坐标,再将A、C两点的坐标代入,运用待定系数法即可求出边AC所在直线的解析式;
(2)已知A,B,C的坐标易知△ABC为等腰直角三角形,所求的三角形与△ABC全等且有一条公共边,分别考虑AB,AC,BC为公共边三种情况.
(2)已知A,B,C的坐标易知△ABC为等腰直角三角形,所求的三角形与△ABC全等且有一条公共边,分别考虑AB,AC,BC为公共边三种情况.
解答: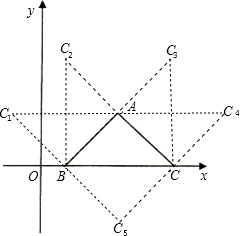 解:(1)设C点的坐标为(x,0).
解:(1)设C点的坐标为(x,0).
∵AB=AC,
∴点A在BC的垂直平分线上,
又∵A点坐标为(3,2),B点坐标为(1,0),
∴
=3,
∴x=5,即C点的坐标为(5,0).
设边AC所在直线的解析式为y=kx+b,则
,
解得
.
故边AC所在直线的解析式y=-x+5;
(2)∵A点坐标为(3,2),B点坐标为(1,0),C点的坐标为(5,0),
∴AB=AC=2
,BC=4,
∴AB2+AC2=BC2,
∴△ABC为等腰直角三角形.
如图所示,符合要求的点有:
C1(-1,2),C2(1,4),C3(5,4),C4(7,2),C5(3,-2).
 解:(1)设C点的坐标为(x,0).
解:(1)设C点的坐标为(x,0).∵AB=AC,
∴点A在BC的垂直平分线上,
又∵A点坐标为(3,2),B点坐标为(1,0),
∴
| 1+x |
| 2 |
∴x=5,即C点的坐标为(5,0).
设边AC所在直线的解析式为y=kx+b,则
|
解得
|
故边AC所在直线的解析式y=-x+5;
(2)∵A点坐标为(3,2),B点坐标为(1,0),C点的坐标为(5,0),
∴AB=AC=2
| 2 |
∴AB2+AC2=BC2,
∴△ABC为等腰直角三角形.
如图所示,符合要求的点有:
C1(-1,2),C2(1,4),C3(5,4),C4(7,2),C5(3,-2).
点评:本题主要考查了运用待定系数法求一次函数的解析式,三角形全等的性质及勾股定理的逆定理,综合性较强,难度中等.注意(2)中应分几种情况讨论,讨论时要做到不重不漏.

练习册系列答案
相关题目
 (2013•天津)如图,将△ABC放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上.
(2013•天津)如图,将△ABC放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上.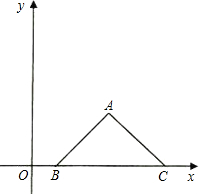 标为(3,2),B点坐标为(1,0).
标为(3,2),B点坐标为(1,0).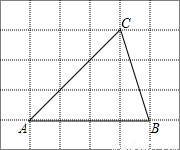
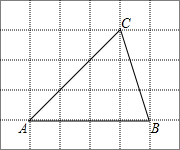 如图,将△ABC放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上.
如图,将△ABC放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上.