题目内容
如图,已知点A,B分别在x轴和y轴上,且OA=OB=3
,点C的坐标是C(
,
),AB与OC相交于点G.点P从O出发以每秒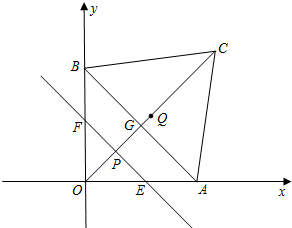 1个单位的速度从O运动到C,过P作直线EF∥AB分别交OA,OB于E,F.解答下列问题:
1个单位的速度从O运动到C,过P作直线EF∥AB分别交OA,OB于E,F.解答下列问题:
(1)直接写出点G的坐标和直线AB的解析式.
(2)若点P运动的时间为t,直线EF在四边形OACB内扫过的面积为s,请求出s与t的函数关系式;并求出当t为何值时,直线EF平分四边形OACB的面积.
(3)设线段OC的中点为Q,P运动的时间为t,求当t为何值时,△EFQ为直角三角形.
| 2 |
| 7 |
| 2 |
| 2 |
| 7 |
| 2 |
| 2 |
 1个单位的速度从O运动到C,过P作直线EF∥AB分别交OA,OB于E,F.解答下列问题:
1个单位的速度从O运动到C,过P作直线EF∥AB分别交OA,OB于E,F.解答下列问题:(1)直接写出点G的坐标和直线AB的解析式.
(2)若点P运动的时间为t,直线EF在四边形OACB内扫过的面积为s,请求出s与t的函数关系式;并求出当t为何值时,直线EF平分四边形OACB的面积.
(3)设线段OC的中点为Q,P运动的时间为t,求当t为何值时,△EFQ为直角三角形.
分析:(1)根据AB与OC相交于点G,以及C点横纵坐标相等得出G点坐标为AB中点,即可得出答案,再利用A,B两点坐标得出解析式即可;
(2)分别根据当0<t≤3时,当3<t<7时,利用相似三角形的性质得出s与t的关系时即可.
(3)利用①当P在线段OQ上,且∠EQF=90°时,以及②当P在线段CQ上,且∠EQF=90°时,利用相似三角形的性质得出即可.
(2)分别根据当0<t≤3时,当3<t<7时,利用相似三角形的性质得出s与t的关系时即可.
(3)利用①当P在线段OQ上,且∠EQF=90°时,以及②当P在线段CQ上,且∠EQF=90°时,利用相似三角形的性质得出即可.
解答:解:(1)G点的坐标是G(
,
),
∵OA=OB=3
,得出A,B两点坐标,
分别为:(3
,0),(0,3
),
代入y=kx+b,
,
解得:
,
即可得出直线AB的解析式为:y=-x+3
…(2分);
(2)∵C的坐标是C(
,
),
∴OC是∠AOB的角平分线.OC=
=7,
又∵OA=OB=3
,
∴AB=
=6,
∴∠BAO=∠ABO=∠BOG=∠AOG=45°,
∴∠AGO=90°,即AB⊥OC,
∴OG=3,
①当0<t≤3时,OP=t,
∵EF∥AB,
∴EF⊥OC,
∴EF=2OP=2t,
∴S=S△OEF=
•EF•OP=
•2t•t=t2…(5分),
②当3<t<7时,OP=t,CP=7-t,CG=7-OG=7-3=4,
∵EF∥AB,
∴△CEF∽△CBA,
∴
=
,
即
=
,
∴EF=
(7-t),
∴S=S四边形OACB-S△CEF=
•AB•CO-
EF•CP,
=
×6×7-
×
(7-t)(7-t),
=-
t2+
t-
,
∴s与t的函数关系式是:
S=
…(7分)
当直线EF平分四边形OABC的面积时有:-
t2+
t-
=
×
×6×7,
整理得:t2-14t+35=0,
解得:x1=7+
>7(不符合题意舍去); x2=7-

∴当t=7-
时,直线EF平分四边形OABC的面积.…(8分)
(3)①如图1,当P在线段OQ上,且∠EQF=90°时,
∵EF∥AB,
∴∠OEF=∠OAB=∠OBA=∠OFE=45°,
∴OE=OF,
又∵∠FOG=∠EOG=45°,OQ=OQ,
∴△OEQ≌△OFQ,
∴∠FQO=∠EQO=45°,
∴∠OFQ=∠FOE=∠FQE=90°,
∴四边形OEQF是正方形,
∴OP=
OQ=
×
=
,
即t=
时,△EFQ为直角三角形,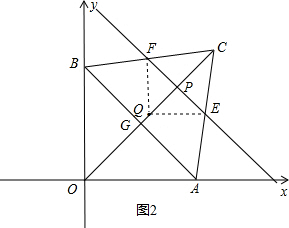
②如图2,当P在线段CQ上,且∠EQF=90°时,
同理可证:△CQF≌△CQE,
∴△QEF是等腰直角三角形,
∴EF=2PQ=2(t-
),
∵EF∥AB,
∴△CEF∽△CBA,
∴
=
,
即
=
,
解得:t=5,
∴当t=
或t=5时,△EFQ为直角三角形.…(12分)
| 3 |
| 2 |
| 2 |
| 3 |
| 2 |
| 2 |
∵OA=OB=3
| 2 |
分别为:(3
| 2 |
| 2 |
代入y=kx+b,
|
解得:
|
即可得出直线AB的解析式为:y=-x+3
| 2 |
(2)∵C的坐标是C(
| 7 |
| 2 |
| 2 |
| 7 |
| 2 |
| 2 |
∴OC是∠AOB的角平分线.OC=
(
|
又∵OA=OB=3
| 2 |
∴AB=
(3
|
∴∠BAO=∠ABO=∠BOG=∠AOG=45°,
∴∠AGO=90°,即AB⊥OC,
∴OG=3,
①当0<t≤3时,OP=t,
∵EF∥AB,
∴EF⊥OC,
∴EF=2OP=2t,
∴S=S△OEF=
| 1 |
| 2 |
| 1 |
| 2 |
②当3<t<7时,OP=t,CP=7-t,CG=7-OG=7-3=4,
∵EF∥AB,
∴△CEF∽△CBA,
∴
| EF |
| BA |
| CP |
| CG |
即
| EF |
| 6 |
| 7-t |
| 4 |
∴EF=
| 3 |
| 2 |
∴S=S四边形OACB-S△CEF=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
=-
| 3 |
| 4 |
| 21 |
| 2 |
| 63 |
| 4 |
∴s与t的函数关系式是:
S=
|
当直线EF平分四边形OABC的面积时有:-
| 3 |
| 4 |
| 21 |
| 2 |
| 63 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
整理得:t2-14t+35=0,
解得:x1=7+
| 14 |
| 14 |

∴当t=7-
| 14 |
(3)①如图1,当P在线段OQ上,且∠EQF=90°时,
∵EF∥AB,
∴∠OEF=∠OAB=∠OBA=∠OFE=45°,
∴OE=OF,
又∵∠FOG=∠EOG=45°,OQ=OQ,
∴△OEQ≌△OFQ,
∴∠FQO=∠EQO=45°,
∴∠OFQ=∠FOE=∠FQE=90°,
∴四边形OEQF是正方形,
∴OP=
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
| 7 |
| 4 |
即t=
| 7 |
| 4 |

②如图2,当P在线段CQ上,且∠EQF=90°时,
同理可证:△CQF≌△CQE,
∴△QEF是等腰直角三角形,
∴EF=2PQ=2(t-
| 7 |
| 2 |
∵EF∥AB,
∴△CEF∽△CBA,
∴
| EF |
| BA |
| CP |
| CG |
即
2(t-
| ||
| 6 |
| 7-t |
| 4 |
解得:t=5,
∴当t=
| 7 |
| 4 |
点评:此题主要考查了一次函数的综合应用以及相似三角形的性质与判定,利用相似三角形的性质得出对应边之间关系得出t的值是解题关键.

练习册系列答案
相关题目
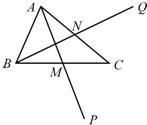 18、如图,已知点M、N分别是△ABC的边BC、AC的中点,点P是点A关于点M的对称点,点Q是点B关于点N的对称点,求证:P、C、Q三点在同一条直线上.
18、如图,已知点M、N分别是△ABC的边BC、AC的中点,点P是点A关于点M的对称点,点Q是点B关于点N的对称点,求证:P、C、Q三点在同一条直线上.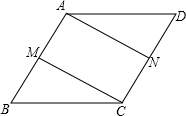 如图,已知点M、N分别是平行四边形ABCD的边AB、DC的中点,求证:∠DAN=∠BCM.
如图,已知点M、N分别是平行四边形ABCD的边AB、DC的中点,求证:∠DAN=∠BCM.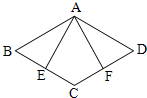 21、如图,已知点E、F分别是菱形ABCD的边AB、AD上,BE=DF,
21、如图,已知点E、F分别是菱形ABCD的边AB、AD上,BE=DF,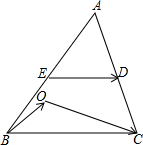 (2013•金山区二模)如图,已知点D,E分别是边AC和AB的中点,设
(2013•金山区二模)如图,已知点D,E分别是边AC和AB的中点,设 如图,已知点E、F分别是AC、AB的中点,其中△AFE的面积为2,则△EFG的面积为
如图,已知点E、F分别是AC、AB的中点,其中△AFE的面积为2,则△EFG的面积为