题目内容
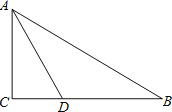
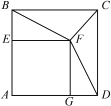
【题目】如图,在矩形纸片![]() 中,
中,![]() ,对折矩形纸片
,对折矩形纸片![]() ,使
,使![]() 与
与![]() 重合,折痕为
重合,折痕为![]() ,展平后再过点
,展平后再过点![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 上的点
上的点![]() ,折痕为
,折痕为![]() .再次展平,连接
.再次展平,连接![]() ,
,![]() ,有下列结论:①
,有下列结论:①![]() ;②
;②![]() 与
与![]() 相似;③
相似;③![]() 的长为
的长为![]() :④若
:④若![]() 分别为线段
分别为线段![]() 上的动点(不包含端点),则
上的动点(不包含端点),则![]() 的最小值是
的最小值是![]() .其中正确结论的序号是__________.
.其中正确结论的序号是__________.
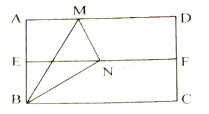
【答案】①②④
【解析】
①如图,连接AN,根据线段垂直平分线的性质得到AN=BN,根据折叠的性质得到AB=BN,推理出△ABN为等边三角形,得到∠ABN=60°,于是得到∠ABM=∠MBN=∠CBN=30°,即结论①正确;
②根据折叠的性质,可得∠BNM=∠BAD=90°,∠BEN=∠AEN=90°,根据相似三角形的判定定理得到△BEN与△BMN相似,即结论②正确;
③解直角三角形得到MN=![]() BN=
BN=![]() ,即结论③错误;
,即结论③错误;
④过A作AQ⊥BN于Q交BM于P,则此时PN+PQ的值最小,且PN+PQ=AQ,解直角三角形得到PN+PQ的最小值是![]() .即结论④正确.
.即结论④正确.
解:①如图,连接AN,
∵EF垂直平分AB,∴AN=BN,
根据折叠的性质,可得AB=BN,
∴AN=AB=BN=2.
∴△ABN为等边三角形,
∴∠ABN=60°,
∴∠ABM=∠MBN=∠CBN=30°,
即结论①正确;
②根据折叠的性质,可得∠BNM=∠BAD=90°,∠BEN=∠AEN=90°,
∴∠BEN=∠BNM,
∵∠MBN=30°,∠EBN=60°,∴∠BMN=60°,
∴∠EBN=∠BMN,
∴△BEN与△BMN相似,
即结论②正确;
③∵∠ABM=∠MBN=30°,BN=AB=2,∠BNM=∠BAM=90°,
∴MN=![]() BN=
BN=![]() ,即结论③错误;
,即结论③错误;
④∵A点和N点关于BM对称,
∴过A点作![]() 于Q交BM于P,
于Q交BM于P,
此时PN+PQ的值最小,且PN+PQ=AQ,
∵∠ABQ=60°,AB=2,
∴AQ=![]() AB=
AB=![]() ,
,
∴PN+PQ的最小值是![]() .
.
即结论④正确.
故答案为①②④.