题目内容
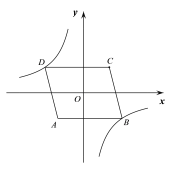
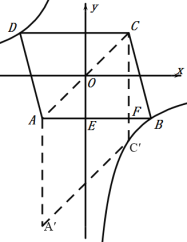
【题目】如图,在平面直角坐标系中,O为□ABCD的对称中心,点A的坐标为(-2,-2),AB=5,AB//x轴,反比例函数y=![]() 的图象经过点D,将□ABCD沿y轴向下平移,使点C的对应点C′落在反比例函数的图象上,则平移过程中线段AC扫过的面积为( )
的图象经过点D,将□ABCD沿y轴向下平移,使点C的对应点C′落在反比例函数的图象上,则平移过程中线段AC扫过的面积为( )
A.10B.18C.20D.24
【答案】C
【解析】
根据O为ABCD的对称中心,AB=5,AB∥x轴交y轴于点E,点A的坐标为(-2,-2),可求点C、B的坐标,进而求出反比例函数的关系式,由平移可求出点C′的坐标,知道平移的距离,即平行四边形的底,再根据点的坐标,可求出平行四边形的高,最后根据面积公式求出结果.
∵AB=5,AB∥x轴交y轴于点E,点A的坐标为(-2,-2),
∴BE=5-2=3,OE=2,
∴B(3,-2)代入反比例函数的关系式得,k=-2×6=-6,
∴反比例函数的解析式为![]() ,
,
∵O为ABCD的对称中心,点A的坐标为(-2,-2),
∴点C的坐标为(2,2),
平移后,如图,
当![]() 时,
时,![]()
∴点C′(2,-3),
∴CC′=2-(-3)=2+3=5,
CC′交AB于F,则AF=AE+EF=2+2=4,
∴平行四边形ACC′A′的面积为5×4=20,
故选:C.

 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案【题目】随着生活节奏的加快以及智能手机的普及,外卖点餐逐渐成为越来越多用户的餐饮消费习惯.由此催生了一批外卖点餐平台,已知某外卖平台的送餐费用与送餐距离有关(该平台只给5千米范围内配送),为调査送餐员的送餐收入,现从该平台随机抽取80名点外卖的用户进行统计,按送餐距离分类统计结果如下表:
送餐距离x(千米) | 0 | 1 | 2 | 3 | 4 |
数量 | 12 | 20 | 24 | 16 | 8 |
(1)从这80名点外卖的用户中任取一名用户,该用户的送餐距离不超过3千米的概率为 ;
(2)以这80名用户送餐距离为样本,同一组数据取该小组数据的中间值(例如第二小组(1<x ≤2)的中间值是1.5),试估计利用该平台点外卖用户的平均送餐距离;
(3)若该外卖平台给送餐员的送餐费用与送餐距离有关,不超过2千米时,每份3元;超过2千米但不超4千米时,每份5元;超过4千米时,每份9元. 以给这80名用户所需送餐费用的平均数为依据,若送餐员一天的目标收入不低于150元,试估计一天至少要送多少份外卖?
【题目】为了强化学生的环保意识,某校团委在全校举办了“保护环境,人人有责”知识竞赛活动,初、高中根据初赛成绩,各选出5名选手组成初中代表队和高中代表队进行复赛,两个队学生的复赛成绩(满分10分)如图所示:
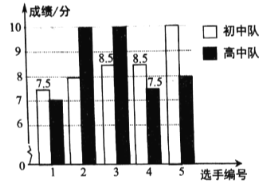
(1)根据图示填写下表:
平均分 | 中位数 | 众数 | 方差 | |
初中队 | 8.5 | 0.7 | ||
高中队 | 8.5 | 10 |
(2)小明同学说:“这次复赛我得了8分,在我们队中排名属中游偏下!”小明是初中队还是高中队的学生?为什么?
(3)结合两队成绩的平均分、中位数和方差,分析哪个对的复赛成绩较好.
【题目】某校开展“文明在行动”的志愿者活动,准备购买某一品牌书包送到希望学校.在![]() 商店,无论一次购买多少,价格均为每个50元.在
商店,无论一次购买多少,价格均为每个50元.在![]() 商店,一次购买数量不超过10个时,价格为每个60元;一次购买数量超过10个时,超出10个部分打八折.设一次购买该品牌书包的数量为x个.
商店,一次购买数量不超过10个时,价格为每个60元;一次购买数量超过10个时,超出10个部分打八折.设一次购买该品牌书包的数量为x个.
(Ⅰ)根据题意填表:
一次购买数量/个 | 5 | 10 | 15 | … |
| 500 | … | ||
| 600 | … |
(Ⅱ)设在![]() 商店花费
商店花费![]() 元,在
元,在![]() 商店花费
商店花费![]() 元,分别求出
元,分别求出![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(Ⅲ)根据题意填空;
①若小丽在![]() 商店和在
商店和在![]() 商店一次购买书包的数量相同,且花费相同,则她在同一商店一次购买书包的数量为______个.
商店一次购买书包的数量相同,且花费相同,则她在同一商店一次购买书包的数量为______个.
②若小丽在同一商店一次购买书包的数量为50个,则她在![]() 两个商店中的______商店购买花费少;
两个商店中的______商店购买花费少;
③若小丽在同一商店一次购买书包花费了1800元,则她在![]() 两个商店中_______商店购买数量多.
两个商店中_______商店购买数量多.