题目内容
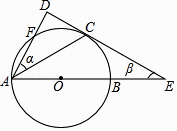
【题目】如图,一次函数y=k1x+5(k1<0)的图象与坐标轴交于A,B两点,与反比例函数y= ![]() (k2>0)的图象交于M,N两点,过点M作MC⊥y轴于点C,已知CM=1.
(k2>0)的图象交于M,N两点,过点M作MC⊥y轴于点C,已知CM=1.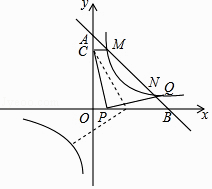
(1)求k2﹣k1的值;
(2)若 ![]() =
= ![]() ,求反比例函数的解析式;
,求反比例函数的解析式;
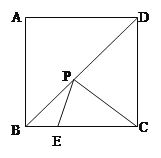
(3)在(2)的条件下,设点P是x轴(除原点O外)上一点,将线段CP绕点P按顺时针或逆时针旋转90°得到线段PQ,当点P滑动时,点Q能否在反比例函数的图象上?如果能,求出所有的点Q的坐标;如果不能,请说明理由.
【答案】
(1)
解:∵MC⊥y轴于点C,且CM=1,
∴M的横坐标为1,
当x=1时,y=k1+5,
∴M(1,k1+5),
∵M在反比例函数的图象上,
∴1×(k1+5)=k2,
∴k2﹣k1=5
(2)
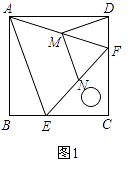
解:如图1,过N作ND⊥y轴于D,
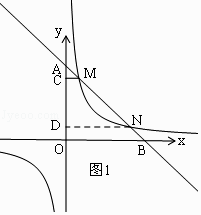
∴CM∥DN,
∴△ACM∽△ADN,
∴ ![]() ,
,
∵CM=1,
∴DN=4,
当x=4时,y=4k1+5,
∴N(4,4k1+5),
∴4(4k1+5)=k2①,
由(1)得:k2﹣k1=5,
∴k1=k2﹣5②,
把②代入①得:4(4k2﹣20+5)=k2,
k2=4;
∴反比例函数的解析式:y= ![]()
(3)
解:当点P滑动时,点Q能在反比例函数的图象上;
如图2,

CP=PQ,∠CPQ=90°,
过Q作QH⊥x轴于H,
易得:△COP≌△PHQ,
∴CO=PH,OP=QH,
由(2)知:反比例函数的解析式:y= ![]() ;
;
当x=1时,y=4,
∴M(1,4),
∴OC=PH=4,
设P(x,0),
∴Q(x+4,x),
当点Q落在反比例函数的图象上时,
x(x+4)=4,
x2+4x+4=8,
x=﹣2± ![]() ,
,
当x=﹣2+2 ![]() 时,x+4=2+2
时,x+4=2+2 ![]() ,如图2,Q(2+2
,如图2,Q(2+2 ![]() ,﹣2+2
,﹣2+2 ![]() );
);

当x=﹣2﹣2 ![]() 时,x+4=2﹣2
时,x+4=2﹣2 ![]() ,如图3,Q(2﹣2
,如图3,Q(2﹣2 ![]() ,﹣2﹣2
,﹣2﹣2 ![]() );
);
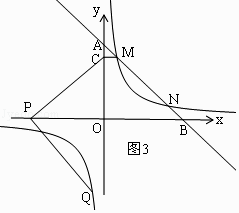
如图4,CP=PQ,∠CPQ=90°,设P(x,0),
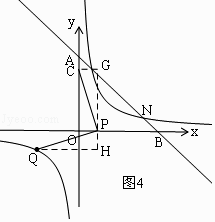
过P作GH∥y轴,过C作CG⊥GH,过Q作QH⊥GH,
易得:△CPG≌△PQH,
∴PG=QH=4,CG=PH=x,
∴Q(x﹣4,﹣x),
同理得:﹣x(x﹣4)=4,
解得:x1=x2=2,
∴Q(﹣2,﹣2),
综上所述,点Q的坐标为(2+2 ![]() ,﹣2+2
,﹣2+2 ![]() )或(2﹣2
)或(2﹣2 ![]() ,﹣2﹣2
,﹣2﹣2 ![]() )或(﹣2,﹣2).
)或(﹣2,﹣2).
【解析】(1)根据点M的坐标代入反比例关系:y= ![]() 中,可得结论;(2)根据△ACM∽△ADN,得
中,可得结论;(2)根据△ACM∽△ADN,得 ![]() ,由CM=1得DN=4,同理得N的坐标,代入反比例函数式中可得k2的值;(3)如图2,点P在x轴的正半轴上时,绕P顺时针旋转到点Q,根据△COP≌△PHQ,得CO=PH,OP=QH,设P(x,0),表示Q(x+4,x),代入反比例函数的关系式中可得Q的两个坐标;
,由CM=1得DN=4,同理得N的坐标,代入反比例函数式中可得k2的值;(3)如图2,点P在x轴的正半轴上时,绕P顺时针旋转到点Q,根据△COP≌△PHQ,得CO=PH,OP=QH,设P(x,0),表示Q(x+4,x),代入反比例函数的关系式中可得Q的两个坐标;
如图3,点P在x轴的负半轴上时;
如图4,点P在x轴的正半轴上时,绕P逆时针旋转到点Q,同理可得结论.
【考点精析】关于本题考查的反比例函数的性质,需要了解性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大才能得出正确答案.

【题目】某中学举行“校园好声音”歌手大赛,初、高中部根据初赛成绩,各选出![]() 名选手组成初中代表队和高中代表队参加学校决赛.每个队
名选手组成初中代表队和高中代表队参加学校决赛.每个队![]() 名选手的决赛成绩如图所示:
名选手的决赛成绩如图所示:

![]() 填表:
填表:
平均数(分) | 中位数(分) | 众数(分) | |
初中代表队 |
|
| |
高中代表队 |
|
|
![]() 结合两队决赛成绩的平均数和中位数,分析哪个代表队的成绩较好;
结合两队决赛成绩的平均数和中位数,分析哪个代表队的成绩较好;
![]() 计算两队决赛成绩的方差,并判断哪个代表队的成绩较为稳定.
计算两队决赛成绩的方差,并判断哪个代表队的成绩较为稳定.
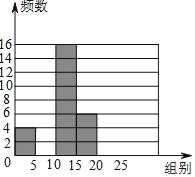
【题目】珠海市某中学开展主题为“我爱阅读”的专题调查活动,为了解学校1200名学生一年内阅读书籍量,随机抽取部分学生进行统计,绘制成如下尚未完成的频数分布表和频数分布直方图.请根据图表,解答下面的问题:
分组 | 频数 | 频率 |
0≤x<5 | 4 | 0.08 |
5≤x<10 | 14 | 0.28 |
10≤x<15 | 16 | a |
15≤x<20 | b | c |
20≤x<25 | 10 | 0.2 |
合计 | d | 1.00 |
(1)a= ,b= c= .
(2)补全频数分布直方图;
(3)根据该样本,估计该校学生阅读书籍数量在15本或15本以上的人数.