题目内容
阅读下列一段话,并解决后面的问题.观察下面一列数:
1,2,4,8,…
我们发现,这一列数从第2项起,每一项与它前一项的比都等于2.
一般地,如果一列数从第2项起,每一项与它前一项的比都等于同一个常数,这一列数就叫做等比数列,这个常数叫做等比数列的公比.
(1)等比数列5,-15,45,…的第4项是
(2)如果一列数a1,a2,a3,a4,…是等比数列,且公比为q,那么根据上述的规定,有
| a2 |
| a1 |
| a3 |
| a2 |
| a4 |
| a3 |
所以a2=a1q
a3=a2q=(a1q)q=a1q2
a4=a3q=(a1q2)q=a1q3
…an=
(3)一个等比数列的第2项都是10,第3项是20,求它的第1项与第4项.
分析:(1)根据题意可得等比数列5,-15,45,…中,从第2项起,每一项与它前一项的比都等于-3;故第4项是45×(-3)=-135;
(2)观察数据可得an=a1qn-1;
(3)根据(1)中的定义,与(2)的关系式,可得q的值进而可得它的第1项与第4项的值.
(2)观察数据可得an=a1qn-1;
(3)根据(1)中的定义,与(2)的关系式,可得q的值进而可得它的第1项与第4项的值.
解答:解:(1)45×(-3)=-135;
(2)an=a1qn-1;
(3)∵a2=10,a3=20;
∴q=
=2;
又∵a2=a1q,a4=a3q
∴a1=5
a4=20×2=40.
(2)an=a1qn-1;
(3)∵a2=10,a3=20;
∴q=
| 20 |
| 10 |
又∵a2=a1q,a4=a3q
∴a1=5
a4=20×2=40.
点评:本题是一道找规律的题目,要求学生通过观察,分析、归纳发现其中的规律,并应用发现的规律解决问题.分析数据获取信息是必须掌握的数学能力,如观察数据可得an=a1qn-1.

练习册系列答案
相关题目
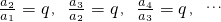
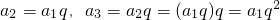 ,
,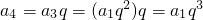 ,…an=______.(用a1与q的代数式表示)
,…an=______.(用a1与q的代数式表示)