题目内容
阅读下列一段话，并解决后面的问题．
观察下面一列数：3，5，7，9，…我们发现这一列数从第2项起，每一项与它前一项的差都等于同一个常数2，这一列数叫做等差数列，这个常数2叫做等差数列的公差．
（1）等差数列3，7，11，…的第五项是
（2）如果一列数a1，a2，a3，…是等差数列，且公差为d，那么根据上述规定，有
a2-a1=d a3-a2=d a4-a3=d …
所以，a2=a1+d；a3=a2+d=（a1+d）+d=a1+2d
a4=a3+d=（a1+2d）+d=a1+3d …
an=
（3）一个等差数列的第二项是107，第三项是135，则它的公差为
观察下面一列数：3，5，7，9，…我们发现这一列数从第2项起，每一项与它前一项的差都等于同一个常数2，这一列数叫做等差数列，这个常数2叫做等差数列的公差．
（1）等差数列3，7，11，…的第五项是
19
19
；（2）如果一列数a1，a2，a3，…是等差数列，且公差为d，那么根据上述规定，有
a2-a1=d a3-a2=d a4-a3=d …
所以，a2=a1+d；a3=a2+d=（a1+d）+d=a1+2d
a4=a3+d=（a1+2d）+d=a1+3d …
an=
a1+（n-1）d
a1+（n-1）d
（用含有 a1与d的代数式表示）（3）一个等差数列的第二项是107，第三项是135，则它的公差为
28
28
，第一项为79
79
，第五项为191
191
．分析：（1）根据等差数列的性质得出第4项与第5项即可；
（2）根据等差数列的特点得出每一项与第一项的关系即可得出规律；
（3）利用等差数列的性质分别求出公差以及各项即可．
（2）根据等差数列的特点得出每一项与第一项的关系即可得出规律；
（3）利用等差数列的性质分别求出公差以及各项即可．
解答：解：（1）等差数列3，7，11，…的公差是4，
故第4项是15，第5项是19；
故答案为：19；
（2）∵a2=a1+d；a3=a2+d=（a1+d）+d=a1+2d
a4=a3+d=（a1+2d）+d=a1+3d …
∴an=a1+（n-1）d．
故答案为：a1+（n-1）d；
（3）∵一个等差数列的第二项是107，第三项是135，
∴则它的公差为：135-107=28，
∴第一项为：107-28=79，
第五项为：79+4×28=191．
故答案为，28，79，191．
故第4项是15，第5项是19；
故答案为：19；
（2）∵a2=a1+d；a3=a2+d=（a1+d）+d=a1+2d
a4=a3+d=（a1+2d）+d=a1+3d …
∴an=a1+（n-1）d．
故答案为：a1+（n-1）d；
（3）∵一个等差数列的第二项是107，第三项是135，
∴则它的公差为：135-107=28，
∴第一项为：107-28=79，
第五项为：79+4×28=191．
故答案为，28，79，191．
点评：此题主要考查了数字变化规律，根据已知得出等差数列的性质进而得出是解题关键．
练习册系列答案
相关题目
，
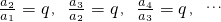
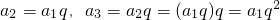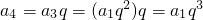，…an=______．（用a1与q的代数式表示）