题目内容
【题目】如图，正方形ABCD的边长为8cm，分别过四个顶点A、B、C、D做四条直线EF、FG、GH、HE，并保证相邻两条直线垂直，相交于E、F、G、H四点，且AE=BF=CG=DH．
（1）求证：四边形EFGH是正方形；
（2）判断无论如何按照上述要求作图，线段EG、AC的中点是否重合，并说明理由；
（3）判断四边形EFGH的面积有无最大值，若有请写出面积最大值，并说明理由．
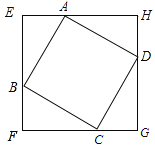
【答案】（1）证明见解析；（2）线段EG、AC的中点重合，理由见解析；（3）面积最大值为128cm2,理由见解析.
【解析】试题分析：（1）由正方形的性质得出∠BAD=∠B=∠BCD=∠D=90°，AB=BC=CD=DA，证出AH=BE=CF=DG，由SAS证明△AEH≌△BFE≌△CGF≌△DHG，得出EH=FE=GF=GH，∠AEH=∠BFE，证出四边形EFGH是菱形，再证出∠HEF=90°，即可得出结论；（2）连接AC、EG，交点为O；先证明△AOE≌△COG，得出OA=OC，证出O为对角线AC、BD的交点，即O为正方形的中心；（3）理由叙述合理即可．
（1）∵相邻两条边互相垂直，
∴∠E=∠F=∠G=∠H=90°，
又∵AE=BF=CG=DH，AB=BC=CD=DA，
∴△EAB≌△FBC≌△GCD≌△HAD，
∴AH=BE=CF=DG，
∴EF=FG=GH=HE，
∵相邻两条边互相垂直，
∴四边形EFGH是正方形；
（2）（证法不唯一）
线段EG、AC的中点重合.
连结EC、AG，
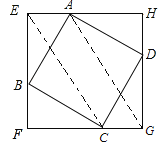
∵AE= CG，且AE∥CG，
∴四边形AECG为平行四边形，
∴线段EG、AC的中点重合.
（3）有最大值，面积最大值为128cm2.如图，
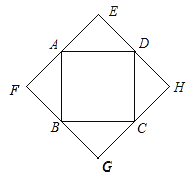
当ABCD分别为各边中点时，四边形EFGH面积最大.（理由叙述合理即可.）
例如：在各种情况中当ABCD分别为各边中点时，四边形EFGH边长为正方形ABCD对角线，其他情况中边长都比对角线小.
