Question

已知：如图，在?ABCD中，BE、CE分别平分∠ABC、∠BCD，E在AD上，BE=12cm，CE=5cm．求?ABCD的周长和面积．

Answer 1

分析：根据角平分线的定义和平行线的性质得到等腰三角形ABE和等腰三角形CDE和直角三角形BCE．根据直角三角形的勾股定理得到BC=13．根据等腰三角形的性质得到AB=CD=

1

2

AD=

1

2

BC=6.5，从而求得该平行四边形的周长；根据直角三角形的面积可以求得平行四边形BC边上的高．

解答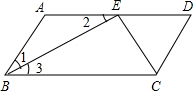：解：∵BE、CE分别平分∠ABC、∠BCD，
∴∠1=∠3=

1

2

∠ABC，∠DCE=∠BCE=

1

2

∠BCD
∵AD∥BC，AB∥CD
∴∠2=∠3，∠BCE=∠CED，∠ABC+∠BCD=180°
∴∠1=∠2，∠DCE=∠CED，∠3+∠BCE=90°
∴AB=AE，CD=DE，∠BEC=90°
在直角三角形BCE中，根据勾股定理得：BC=13
根据平行四边形的对边相等，得到：AB=CD，AD=BC
∴平行四边形的周长等于：13+13+13=39．
作EF⊥BC于F．根据直角三角形的面积公式得：EF=

BE•CE

BC

=

60

13

所以平行四边形的面积=

60

13

×13=60．
即平行四边形的周长为39cm，面积为60cm²．

点评：本题主要考查了平行四边形的性质，在平行四边形中，当出现角平分线时，一般可构造等腰三角形，进而利用等腰三角形的性质解题．