题目内容
【题目】如图,矩形ABCD的对角线AC、BD交于点O,且DE∥AC,CE∥BD. 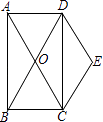
(1)求证:四边形OCED是菱形;
(2)若∠BAC=30°,AC=4,求菱形OCED的面积.
【答案】
(1)证明:∵CE∥OD,DE∥OC,
∴四边形OCED是平行四边形,
∵矩形ABCD,∴AC=BD,OC= ![]() AC,OD=
AC,OD= ![]() BD,
BD,
∴OC=OD,
∴四边形OCED是菱形
(2)解:在矩形ABCD中,∠ABC=90°,∠BAC=30°,AC=4,
∴BC=2,
∴AB=DC=2 ![]() ,
,
连接OE,交CD于点F,
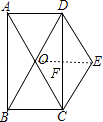
∵四边形ABCD为菱形,
∴F为CD中点,
∵O为BD中点,
∴OF= ![]() BC=1,
BC=1,
∴OE=2OF=2,
∴S菱形OCED= ![]() ×OE×CD=
×OE×CD= ![]() ×2×2
×2×2 ![]() =2
=2 ![]()
【解析】(1)根据平行四边形的判定得出四边形OCED是平行四边形,根据矩形的性质求出OC=OD,根据菱形的判定得出即可.(2)解直角三角形求出BC=2.AB=DC=2 ![]() ,连接OE,交CD于点F,根据菱形的性质得出F为CD中点,求出OF=
,连接OE,交CD于点F,根据菱形的性质得出F为CD中点,求出OF= ![]() BC=1,求出OE=2OF=2,求出菱形的面积即可.
BC=1,求出OE=2OF=2,求出菱形的面积即可.

练习册系列答案
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目