题目内容
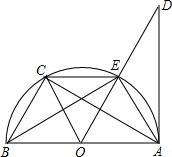
如图1,一辆汽车的背面,有一种特殊形状的刮雨器,忽略刮雨器的宽度可抽象为一条折线OAB,如图2所示,量得连杆OA长为10cm,雨刮杆AB长为48cm,∠OAB=1200.若启动一次刮雨器,雨刮杆AB正好扫到水平线CD的位置,如图3所示.

(1)求雨刮杆AB旋转的最大角度及O、B两点之间的距离;(结果精确到0.01)
(2)求雨刮杆AB扫过的最大面积.(结果保留π的整数倍)
(参考数据:sin60°= ,cos60°=
,cos60°= ,tan60°=
,tan60°=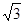 ,
, ≈26.851,可使用科学计算器)
≈26.851,可使用科学计算器)

(1)求雨刮杆AB旋转的最大角度及O、B两点之间的距离;(结果精确到0.01)
(2)求雨刮杆AB扫过的最大面积.(结果保留π的整数倍)
(参考数据:sin60°=
 ,cos60°=
,cos60°= ,tan60°=
,tan60°=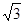 ,
, ≈26.851,可使用科学计算器)
≈26.851,可使用科学计算器)解:(1)∵从点A 旋转到点C为1800,
∴雨刮杆AB旋转的最大角度为1800。
连接OB,过O点作AB的垂线交BA的延长线于EH,

∵∠OAB=1200°,∴∠OAE=60°。
在Rt△OAE中,∵∠OAE=600°,OA=10,
∴ ,
,
 。
。
∵AB=48,∴EB=AE+AB=53。
在Rt△OEB中,∵OE= ,EB=53,
,EB=53,
∴ (cm)。
(cm)。
∴O、B两点之间的距离为53.70 cm。
(2)∵雨刮杆AB旋转180°得到CD,即△OCD与△OAB关于点O中心对称,
∴△BAO≌△OCD。∴S△BAO=S△OCD。
∴雨刮杆AB扫过的最大面积S= π(OB2-OA2) =1392π(cm2)。
π(OB2-OA2) =1392π(cm2)。
∴雨刮杆AB旋转的最大角度为1800。
连接OB,过O点作AB的垂线交BA的延长线于EH,

∵∠OAB=1200°,∴∠OAE=60°。
在Rt△OAE中,∵∠OAE=600°,OA=10,
∴
 ,
, 。
。∵AB=48,∴EB=AE+AB=53。
在Rt△OEB中,∵OE=
 ,EB=53,
,EB=53,∴
 (cm)。
(cm)。∴O、B两点之间的距离为53.70 cm。
(2)∵雨刮杆AB旋转180°得到CD,即△OCD与△OAB关于点O中心对称,
∴△BAO≌△OCD。∴S△BAO=S△OCD。
∴雨刮杆AB扫过的最大面积S=
 π(OB2-OA2) =1392π(cm2)。
π(OB2-OA2) =1392π(cm2)。试题分析:(1)AB旋转的最大角度为180°;在△OAB中,已知两边及其夹角,可求出另外两角和一边,只不过它不是直角三角形,需要转化为直角三角形来求解,由∠OAB=1200想到作AB边上的高,得到一个含600角的Rt△OAE和一个非特殊角的Rt△OEB。在Rt△OAE中,已知∠OAE=600,斜边OA=10,可求出OE、AE的长,从而求得Rt△OEB中EB的长,再由勾股定理求出斜边OB的长。
(2)根据旋转的性质可知,雨刮杆AB扫过的最大面积就是一个半圆环的面积(以OB、OA为半径的半圆面积之差)。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的半径为5,点
的半径为5,点 到圆心
到圆心 ,如果过点
,如果过点
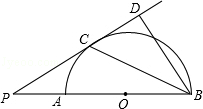
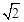 ,求BD的长.
,求BD的长.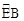 的中点,则下列结论不成立的是
的中点,则下列结论不成立的是