题目内容
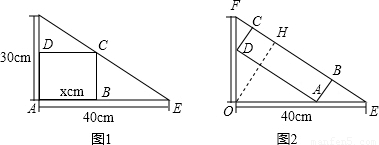
对于题目“如图1,在一个直角三角形的内部作矩形ABCD,其中AB和AD在两直角边上,设AB=xcm,矩形ABCD的面积为ycm2,当x取何值时,y的值最大,最大值是多少?”(答案是当x=20时,y的值最大,最大值是300).小华同学提出了如下两个问题,你能帮助他解决吗?如果按图2使矩形的一边BC在斜边EF上,如何解答此时求出来的最大值仍是300cm2吗?你能肯定图1和图2中的两个面积最大的矩形全等吗?请说明理由.
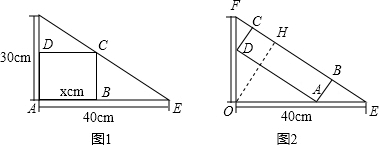
分析:①已知了AB=x,可在Rt△ABE中,用AB的长和∠E的正弦值求出AE的长,进而可表示出AC的长,同理可在Rt△AOD中,用AO的长和∠E的余弦函数求出AD的长,进而可根据矩形的面积公式得出y、x的函数关系式,根据函数的性质即可求出S的最大值为300,以及此时x的值.(也可用相似三角形来求AD的长,方法不唯一).
②先根据①和②函数求出矩形各自的长和宽,然后比较即可.
②先根据①和②函数求出矩形各自的长和宽,然后比较即可.
解答:解:如图2:设AB=xcm,矩形ABCD的面积为ycm2
在Rt△OEF中,sin∠E=
,
∵AB=x,∴AE=AB÷sin∠E=
x,
AO=40-AE=40-
x,
AD=AO÷cos∠DAO=AO÷cos∠E=
(40-
x)=50-
x,
∴y=AD×AB=(50-
x)x,即y=-
x2+50x
配方整理,得y=-
(x-12)2+300,
当x=12cm时,y最大=300cm2
此时矩形ABCD的长BC=25cm,显然图①和图②中的矩形ABCD的面积为300cm2,
由于图①中的矩形的长和宽分别为15cm、20cm,图②中的矩形的长和宽分别为25cm、12cm,
所以图①和图②中的矩形不全等.
在Rt△OEF中,sin∠E=
| 3 |
| 5 |
∵AB=x,∴AE=AB÷sin∠E=
| 5 |
| 3 |
AO=40-AE=40-
| 5 |
| 3 |
AD=AO÷cos∠DAO=AO÷cos∠E=
| 5 |
| 4 |
| 5 |
| 3 |
| 25 |
| 12 |
∴y=AD×AB=(50-
| 25 |
| 12 |
| 25 |
| 12 |
配方整理,得y=-
| 25 |
| 12 |
当x=12cm时,y最大=300cm2
此时矩形ABCD的长BC=25cm,显然图①和图②中的矩形ABCD的面积为300cm2,
由于图①中的矩形的长和宽分别为15cm、20cm,图②中的矩形的长和宽分别为25cm、12cm,
所以图①和图②中的矩形不全等.
点评:本题是二次函数综合题,考查了图象面积的求法,矩形的性质等知识点.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
根据提示完成解答:
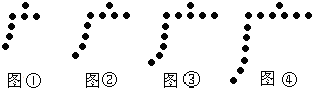
题目:如图①,②,③,④,…,是用围棋棋子按照某种规律摆成的一行“广”字,按照这种规律,第5个“广”字中的棋子个数是________,第n个“广”字中的棋子个数是________
 y
y
提示:
(1)将图形序号1,2,3,4,…,看成变量x,相应图形中棋子个数看成是另一个变量y,由于对于每一个x的值,y都有________与它对应,从而y是x的函数.
(2)列表
| x | … | 1 | 2 | 3 | 4 | … |
| y | … | 7 | 9 | 11 | 13 | … |
在右边的直角坐标系中描出相应的点,并且用光滑的线相连.
(4)猜测:根据图象可以猜测y是x的一次函数.据此可以求出y与x之间的函数关系式为________.
(5)检验:将另外点的坐标代入成立吗?答:________(填写“成立”或者“不成立”)
(6)由上面的解答可以知道,题目中的2个空白处应该分别填写________、________.

 y
y
 图)
图)