题目内容
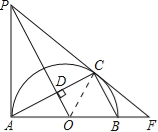
【题目】如图，AB，AC分别是半⊙O的直径和弦，OD⊥AC于点D，过点A作半⊙O的切线AP，AP与OD的延长线交于点P．连接PC并延长与AB的延长线交于点F．
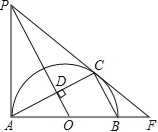
（1）求证：PC是半⊙O的切线；
（2）若∠CAB=30°，AB=10，求线段BF的长．
【答案】见解析；5.
【解析】试题（1）、连接OC，可以证得△OAP≌△OCP，利用全等三角形的对应角相等，以及切线的性质定理可以得到：∠OCP=90°，即OC⊥PC，即可证得；（2）、依据切线的性质定理可知OC⊥PE，然后通过解直角三角函数，求得OF的值，再减去圆的半径即可．
试题解析：（1）、连接OC，
∵OD⊥AC，OD经过圆心O，
∴AD=CD，
∴PA=PC，
在△OAP和△OCP中，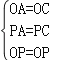
，
∴△OAP≌△OCP（SSS），
∴∠OCP=∠OAP
∵PA是⊙O的切线，
∴∠OAP=90°．
∴∠OCP=90°，
即OC⊥PC
∴PC是⊙O的切线．
（2）、∵AB是直径，
∴∠ACB=90°，
∵∠CAB=30°，
∴∠COF=60°，
∵PC是⊙O的切线，AB=10，
∴OC⊥PF，OC=OB=
AB=5，
∴OF=
=10，
∴BF=OF﹣OB=5．
练习册系列答案
阅读快车系列答案
相关题目
