题目内容
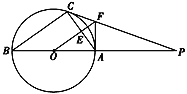
【题目】如图,△ABC内接于⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于点E,交PC于点F,连结AF.
(1)判断AF与⊙O的位置关系并说明理由;
(2)若AC=24,AF=15,求sinB.
【答案】(1) AF与⊙O相切 理由见解析;(2)![]()
【解析】试题分析:(1)连接OC,先证∠OCF=90°,再证明△OAF≌△OCF,得出∠OAF=∠OCF=90°即可;
(2)先求出AE、EF,再证明△OAE∽△AFE,得出比例式![]() ,可求出半径,进而求出直径,由三角函数的定义即可得出结论.
,可求出半径,进而求出直径,由三角函数的定义即可得出结论.
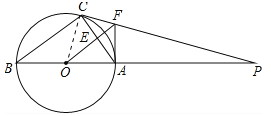
试题解析:解:(1)AF与⊙O相切.理由如下:
连接OC.如图所示.∵PC是⊙O的切线,∴OC⊥PC,∴∠OCF=90°.∵OF∥BC,∴∠B=∠AOF,∠OCB=∠COF.∵OB=OC,∴∠B=∠OCB,∴∠AOF=∠COF.在△OAF和△OCF中,∵OA=OC,∠AOF=∠COF,OF=OF,∴△OAF≌△OCF(SAS),∴∠OAF=∠OCF=90°,∴AF与⊙O相切;
(2)∵△OAF≌△OCF,∴∠OAE=∠COE,∴OE⊥AC,AE=![]() AC=12,∴EF=
AC=12,∴EF=![]() .∵∠OAF=90°,∴△OAE∽△AFE,∴
.∵∠OAF=90°,∴△OAE∽△AFE,∴![]() ,即
,即![]() ,∴OA=20,∴AB=40,sinB=
,∴OA=20,∴AB=40,sinB=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目