题目内容
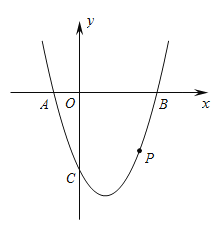
【题目】已知抛物线y=ax2+bx+3经过点A(1,0)和点B(﹣3,0),与y轴交于点C,点P为第二象限内抛物线上的动点.
(1)抛物线的解析式为 ,抛物线的顶点坐标为 ;
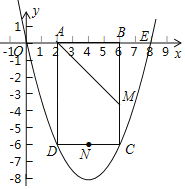
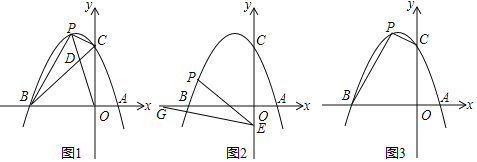
(2)如图1,连接OP交BC于点D,当S△CPD:S△BPD=1:2时,请求出点D的坐标;
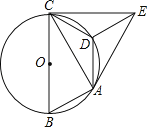
(3)如图2,点E的坐标为(0,﹣1),点G为x轴负半轴上的一点,∠OGE=15°,连接PE,若∠PEG=2∠OGE,请求出点P的坐标;
(4)如图3,是否存在点P,使四边形BOCP的面积为8?若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】(1)y=﹣x2﹣2x+3,顶点坐标为(﹣1,4);(2)点D(﹣1,2);(3)点P(![]() ,
,![]() )(4)不存在,理由见解析.
)(4)不存在,理由见解析.
【解析】
(1)利用待定系数法可求得函数的表达式,再通过配方即可求得顶点坐标;
(2)又S△CPD:S△BPD=1:2,可得BD=![]() BC=
BC=![]() ×
×![]() =
=![]() ,再利用解直角三角形的知识即可求得答案;
,再利用解直角三角形的知识即可求得答案;
(3)设直线PE交x轴于点H,∠OGE=15°,∠PEG=2∠OGE=30°,则∠OHE=45°,故OH=OE=1,解由①②构成的方程组即可求得答案;
(4)连接BC,过点P作y轴的平行线交BC于点H,设点P(x,﹣x2﹣2x+3),点H(x,x+3),则S四边形BOCP=S△OBC+S△PBC=![]() ×3×3+
×3×3+![]() (﹣x2﹣2x+3﹣x﹣3)×3=8,得到关于x的一元二次方程,根据方程解的情况即可得结论.
(﹣x2﹣2x+3﹣x﹣3)×3=8,得到关于x的一元二次方程,根据方程解的情况即可得结论.
(1)∵抛物线y=ax2+bx+3经过点A(1,0)和点B(﹣3,0),
∴![]() ,
,
∴![]() ,
,
∴抛物线的表达式为:y=﹣x2﹣2x+3…①,
y=﹣x2﹣2x+3=-(x+1)2+4,
∴顶点坐标为(﹣1,4);
(2)设点D坐标为(xD,yD),∵OB=OC,∠BOC=90°,
∴∠CBO=45°,BC=![]() ,
,
∵S△CPD:S△BPD=1:2,
∴BD:DC=2:1,
∴BD=![]() BC=
BC=![]() ×
×![]() =
=![]() ,
,
∴xD=-3+ BDcos∠CBO=-3+2=-1, yD=BDsin∠CBO=2,
∴点D(﹣1,2);
(3)如图2,设直线PE交x轴于点,
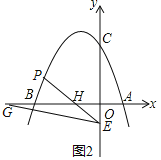
∵∠OGE=15°,∠EOG=90°,
∴∠OEG=90°-15°=75°,
∵∠PEG=2∠OGE,
∴∠PEG=2∠OGE=30°,
∴∠OHE=∠OGE+∠PEG=45°,∠HEO=∠OEG-∠PEG=45°,
∴OH=OE=1,
∴H(-1,0),
设直线HE的解析式为y=mx+n,把H(-1,0)、E(0,-1)分别代入得![]() ,
,
解得![]() ,
,
∴直线HE的表达式为:y=﹣x﹣1…②,
联立①②并解得: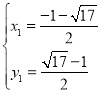 ,
,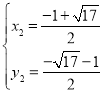 (舍去),
(舍去),
故点P(![]() ,
,![]() );
);
(4)不存在,理由:
如图3,连接BC,过点P作y轴的平行线交BC于点H,
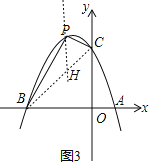
直线BC的表达式为:y=x+3,
设点P(x,﹣x2﹣2x+3),点H(x,x+3),
则S四边形BOCP=S△OBC+S△PBC=![]() ×3×3+
×3×3+![]() (﹣x2﹣2x+3﹣x﹣3)×3=8,
(﹣x2﹣2x+3﹣x﹣3)×3=8,
整理得:3x2+9x+7=0,
解得:△<0,故方程无解,
则不存在满足条件的点P.