Question

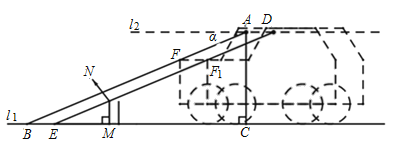
【题目】如图，在四边形ABCD中，点E和点F是对角线AC上的两点，AE＝CF，DF＝BE，且DF∥BE，过点C作CG⊥AB交AB的延长线于点G．

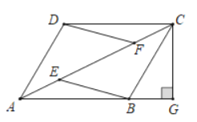
（1）求证：四边形ABCD是平行四边形；（2）若tan∠CAB＝，∠CBG＝45°，BC＝4，则ABCD的面积是　 　．

Answer 1

【答案】（1）见解析；（2）24．

【解析】

（1）根据已知条件得到AF＝CE，根据平行线的性质得到∠DFA＝∠BEC，根据全等三角形的性质得到AD＝CB，∠DAF＝∠BCE，于是得到结论；

（2）根据已知条件得到△BCG是等腰直角三角形，求得BG＝CG＝4，解直角三角形得到AG＝10，根据平行四边形的面积公式即可得到结论．

（1）证明：∵AE＝CF，

∴AE+EF＝CF+EF，

即AF＝CE，

∵DF∥BE，

∴∠DFA＝∠BEC，

∵DF＝BE，

∴△ADF≌△CBE（SAS），

∴AD＝CB，∠DAF＝∠BCE，

∴AD∥CB，

∴四边形ABCD是平行四边形；

（2）解：∵CG⊥AB，

∴∠G＝90°，

∵∠CBG＝45°，

∴△BCG是等腰直角三角形，

∵BC＝4，

∴BG＝CG＝4，

∵tan∠CAB＝，

∴AG＝10，

∴AB＝6，

∴ABCD的面积＝6×4＝24，

故答案为：24．