题目内容
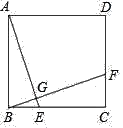
【题目】如图，ABCD为矩形纸片，E、F分别为AB、DC上的点，将此矩形两次翻折，RM和FN为折痕，其中
、
分别为A、D的对应点；且点在射线EF上；
、
分别为B、C的对应点，且点在射线FE上.
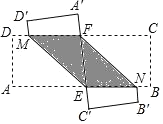
（1）求证：四边形ENFM为平行四边形；
（2）若四边形ENFM为菱形，求∠EMF的度数．
【答案】（1）见解析；（2）60°
【解析】
（1）根据翻折的性质和平行四边形的判定证明即可；
（2）根据菱形的性质和等边三角形的判定和性质解答即可．
证明：(1)∵矩形ABCD，
∴AB//CD，
∴∠CFE=∠AEF，
由翻折可得：∠AEM=∠MEF，∠CFN=∠EFN，
∴∠MEF=∠EFN，
∴ME//FN，
∴四边形ENFM是平行四边形；
(2)∵四边形ENFM为菱形，
∴MF=ME，
∴∠MFE=∠MEF，
∵AB//CD，
∴∠MFE=∠FEN，
∵∠AEM=∠MEF，
∵∠AEM+∠MEF+∠FEN=180，
∴∠AEM=60°，
∴∠EMF=60°．
练习册系列答案
阅读快车系列答案
相关题目
