题目内容
【题目】如图,小明坐在堤边A处垂钓,河堤AC与水平面的夹角为30°,AC的长为 ![]() 米,钓竿AO与水平线的夹角为60°,其长为3米,若AO与钓鱼线OB的夹角为60°,求浮漂B与河堤下端C之间的距离.
米,钓竿AO与水平线的夹角为60°,其长为3米,若AO与钓鱼线OB的夹角为60°,求浮漂B与河堤下端C之间的距离.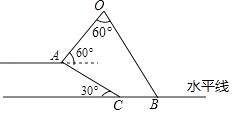
【答案】解:延长OA交BC于点D.
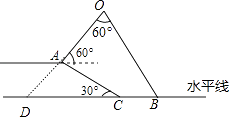
∵AO的倾斜角是60°,
∴∠ODB=60°.
∵∠ACD=30°,
∴∠CAD=180°﹣∠ODB﹣∠ACD=90°.
在Rt△ACD中,AD=ACtan∠ACD= ![]()
![]() =
= ![]() (米),
(米),
∴CD=2AD=3米,
又∵∠O=60°,
∴△BOD是等边三角形,
∴BD=OD=OA+AD=3+ ![]() =4.5(米),
=4.5(米),
∴BC=BD﹣CD=4.5﹣3=1.5(米).
答:浮漂B与河堤下端C之间的距离为1.5米.
【解析】延长OA交BC于点D.先由倾斜角定义及三角形内角和定理求出∠CAD=180°﹣∠ODB﹣∠ACD=90°.解Rt△ACD,得出AD的长度CD的长度,再证明△BOD是等边三角形,得BD=OD=OA+AD =4.5(米),然后根据BC=BD﹣CD得出答案。

练习册系列答案
相关题目
【题目】新冠肺炎疫情期间,某口罩厂为生产更多的口罩满足疫情防控需求,决定拨款456万元购进A,B两种型号的口罩机共30台.两种型号口罩机的单价和工作效率分别如下表:
单价/万元 | 工作效率/(只/h) | |
A种型号 | 16 | 4000 |
B种型号 | 14.8 | 3000 |
(1)求购进A,B两种型号的口罩生产线各多少台.
(2)现有200万只口罩的生产任务,计划安排新购进的口罩机共15台同时进行生产.若工厂的工人每天工作8h,则至少租用A种型号的口罩机多少台才能在5天内完成任务?