题目内容
【题目】在矩形ABCD中,AB=1,AD=![]() ,AF平分∠DAB,过C点作CE⊥BD于E,延长AF.EC交于点H,下列结论中:①AF=FH;②BO=BF;③CA=CH;④BE=3ED.正确的是( )
,AF平分∠DAB,过C点作CE⊥BD于E,延长AF.EC交于点H,下列结论中:①AF=FH;②BO=BF;③CA=CH;④BE=3ED.正确的是( )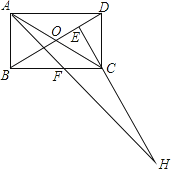
A.②③
B.③④
C.①②④
D.②③④
【答案】D
【解析】∵AB=1,AD= ![]() ,
,
∴BD=AC=2,OB=OA=OD=OC=1.
∴△OAB,△OCD为正三角形.
AF平分∠DAB,∴∠FAB=45°,即△ABF是一个等腰直角三角形.
∴BF=AB=1,BF=BO=1.
∵AF平分∠DAB,
∴∠FAB=45°,
∴∠CAH=45°﹣30°=15°.
∵∠ACE=30°(正三角形上的高的性质)∴∠AHC=15°,
∴CA=CH
由正三角形上的高的性质可知:DE=OD÷2,OD=OB,
∴BE=3ED.
所以正确的是②③④.
故选D.
【考点精析】掌握角平分线的性质定理和等腰三角形的性质是解答本题的根本,需要知道定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上;等腰三角形的两个底角相等(简称:等边对等角).

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目