题目内容
【题目】某修理厂需要购进甲、乙两种配件，经调查，每个甲种配件的价格比每个乙种配件的价格少0.4万元，且用16万元购买的甲种配件的数量与用24万元购买的乙种配件的数量相同．
（1）求每个甲种配件、每个乙种配件的价格分别为多少万元；
（2）现投入资金40万元，根据维修需要预测，甲种配件要比乙种配件至少要多11件，问乙种配件最多可购买多少件．
【答案】（1）每个甲种配件的价格为0.8万元，每个乙种配件的价格为1.2万元；（2）15
【解析】
（1）设每个乙种配件的价格为x万元，则每个甲种配件的价格为（x-0.4）万元，根据数量=总价÷单价结列出于x的分式方程，解之经检验后即可得出结论；
（2）设购买甲种配件m件，购买乙种配件n件，根据总价=单价×购买数量，即可得出m=100-1.5n，再结合甲种配件要比乙种配件至少要多22件，即可得出关于n的一元一次不等式，解之结合m，n均为非负整数可得出n的最大值．
（1）设每个乙种配件的价格为x万元，则每个甲种配件的价格为（x﹣0.4）万元，
根据题意得：
，
解得：x＝1.2，
经检验，x＝1.2是原分式方程的解，
∴x﹣0.4＝1.2﹣0.4＝0.8．
答：每个甲种配件的价格为0.8万元、每个乙种配件的价格为1.2万元．
（2）设购买甲种配件m件，购买乙种配件n件，
根据题意得：0.8m+1.2n＝40，
∴m＝50﹣1.5n，
又∵甲种配件要比乙种配件至少要多11件，
∴m﹣n≥11，
∴50﹣1.5n﹣n≥11，
∴n≤15.6，
∵m，n均为非负整数，
∴n的最大值为15．
答：乙种配件最多可购买15件．
【题目】商贸公司购进某种水果的成本为20元/kg，经过市场调研发现，这种水果在未来48天的销售单价p（元/kg）与时间t（天）之间的函数关系式为p=
，且其日销售量y（kg）与时间t（天）的关系如表：
时间t（天） | 1 | 3 | 6 | 10 | 20 | 40 | … |
日销售量y（kg） | 118 | 114 | 108 | 100 | 80 | 40 | … |
（1）已知y与t之间的变化规律符合一次函数关系，试求在第30天的日销售量是多少？
（2）问哪一天的销售利润最大？最大日销售利润为多少？
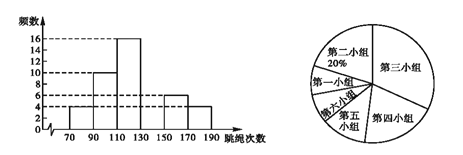
【题目】为了传承中国传统文化，某校组织了一次全体学生“汉字听写”大赛，每位学生听写汉字39个，随机抽取了部分学生的听写结果作为样本进行整理，绘制成如下的统计图表：
组别 | 正确字数x | 人数 |
A |
| 10 |
B |
| 15 |
C |
| 25 |
D |
| m |
E |
| n |
根据以上信息完成下列问题：
（1）统计表中的
________，
________，并补全条形统计图；扇形统计图中“C组“所对应的圆心角的度数是________；
（2）已知该校共有600名学生，如果听写正确的字的个数不少于24个定为合格，请你估计该校本次听写比赛合格的学生人数．
【题目】目前节能灯在城市已基本普及，今年山东省面向县级及农村地区推广节能灯，为响应号召，某商场计划购进甲、乙两种节能灯共1200只，这两种节能灯的进价、售价如下表：
进价(元/只) | 售价(元/只) | |
甲 | 25 | 30 |
乙 | 45 | 60 |
(1)如何进货，进货款恰好为46000元？
(2)如何进货，商场销售完节能灯时获利最多且不超过进货价的30%，此时利润为多少元？
